
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{{\sqrt{5}}}{2}$ |
分析 求得双曲线的渐近线方程,设P(m,n)是双曲线上任一点,设过P平行于x+ay=0的直线为l,求得l的方程,联立另一条渐近线可得交点A,|OA|,求得P到OA的距离,由平行四边形的面积公式,化简整理,解方程可得a=2,求得c,进而得到所求双曲线的离心率.
解答 解:由双曲线方程可得渐近线方程x±ay=0,
设P(m,n)是双曲线上任一点,设过P平行于x+ay=0的直线为l,
则l的方程为:x+ay-m-an=0,l与渐近线x-ay=0交点为A,
则A($\frac{m+an}{2}$,$\frac{m+an}{2a}$),|OA|=|$\frac{m+an}{2}$|$\sqrt{1+\frac{1}{a^2}}$,
P点到OA的距离是:$d=\frac{{|{m-an}|}}{{\sqrt{1+{a^2}}}}$,
∵|OA|•d=1,∴|$\frac{m+an}{2}$|•$\sqrt{1+\frac{1}{a^2}}$.$\frac{{|{m-an}|}}{{\sqrt{1+{a^2}}}}$=1,
∵$\frac{m^2}{a^2}-{n^2}=1$,∴a=2,∴$c=\sqrt{5}$,
∴$e=\frac{{\sqrt{5}}}{2}$.
故选:D.
点评 本题考查双曲线的离心率的求法,注意运用渐近线方程和两直线平行的条件:斜率相等,联立方程求交点,考查化简整理的运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
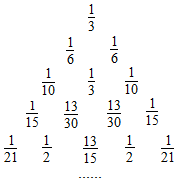
| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{7}{12}$ | D. | $\frac{11}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$+1 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com