
分析 (1)求导数,由f(x)在x=0处取得极值,可得f′(0)=0,解得a;
(2)“分离参数法”:由f(x)在[3,+∞)上为减函数,可得f′(x)≤0,可得a≥$\frac{-3{x}^{2}+6x}{x-1}$,在[3,+∞)上恒成立.令u(x)=$\frac{-3{x}^{2}+6x}{x-1}$,利用导数研究其最大值即可.
解答 解:(1)f′(x)=$\frac{-3{x}^{2}+(6-a)x+a}{{e}^{x}}$,
∵f(x)在x=0处取得极值,∴f′(0)=0,解得a=0;
(2)由f(x)在[3,+∞)上为减函数,∴f′(x)≤0,
可得a≥$\frac{-3{x}^{2}+6x}{x-1}$,在[3,+∞)上恒成立.
令u(x)=$\frac{-3{x}^{2}+6x}{x-1}$,u′(x)=$\frac{-3[(x-1)^{2}+1]}{(x-1)^{2}}$<0,
∴u(x)在[3,+∞)上单调递减,
∴a≥u(3)=-$\frac{9}{2}$.
因此a的取值范围为:[-$\frac{9}{2}$,+∞).
点评 本题考查了导数的运算法则、利用导数研究函数的单调性极值,考查了“分离参数法”、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
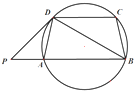 如图,圆内接四边形ABCD满足AB∥CD,P在BA的延长线上,且PD2=PA•PB.若BD=2$\sqrt{2}$,PD=CD=2.
如图,圆内接四边形ABCD满足AB∥CD,P在BA的延长线上,且PD2=PA•PB.若BD=2$\sqrt{2}$,PD=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{5}$ | B. | 1 | C. | $\frac{5}{11}$ | D. | ${(\frac{11}{5})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 78 16 65 72 08 20 63 14 07 02 43 69 97 28 01 98 |
| 32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81 |
| A. | 08 | B. | 14 | C. | 07 | D. | 02 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{24}{25}$ | B. | -$\frac{4}{5}$ | C. | $\frac{24}{25}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e-1 | B. | e | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 0或1 | C. | -1或0 | D. | 1或-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com