
【题目】如图,在棱长为3的正方体![]() 中,
中,![]() .
.
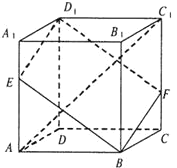
![]() 求两条异面直线
求两条异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
![]() 求直线
求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)以D为原点,建立空间直角坐标系D-xyz,则我们易求出已知中,各点的坐标,进而求出向量![]() ,
,![]() 的坐标.代入向量夹角公式,结合异面直线夹角公式,即可得到答案.
的坐标.代入向量夹角公式,结合异面直线夹角公式,即可得到答案.
(2)设出平面BED1F的一个法向量为![]() ,根据法向量与平面内任一向量垂直,数量积为0,构造方程组,求出平面BED1F的法向量为
,根据法向量与平面内任一向量垂直,数量积为0,构造方程组,求出平面BED1F的法向量为![]() 的坐标,代入线面夹角向量公式,即可求出答案.
的坐标,代入线面夹角向量公式,即可求出答案.
解:(1)以D为原点,建立空间直角坐标系D-xyz如图所示:
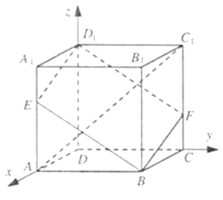
则A(3,0,0),C1=(0,3,3),D1=(0,0,3),E(3,0,2)
∴![]() =(-3,3,3),
=(-3,3,3),![]() =(3,0,-1)
=(3,0,-1)
∴cosθ=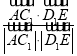 =
=![]() =-
=-![]()
则两条异面直线AC1与D1E所成角的余弦值为![]()
(2)B(3,3,0),![]() =(0,-3,2),
=(0,-3,2),![]() =(3,0,-1)
=(3,0,-1)
设平面BED1F的一个法向量为![]() =(x,y,z)
=(x,y,z)
由 得
得![]()
令x=1,则![]() =(1,2,3)
=(1,2,3)
则直线AC1与平面BED1F所成角的正弦值为
|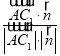 |=
|=![]() =
=![]()


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 直角坐标方程;
直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学将收集到的六组数据制作成散点图如图所示,并得到其回归直线的方程为![]() ,计算其相关系数为
,计算其相关系数为![]() ,相关指数为
,相关指数为![]() .经过分析确定点
.经过分析确定点![]() 为“离群点”,把它去掉后,再利用剩下的5组数据计算得到回归直线的方程为
为“离群点”,把它去掉后,再利用剩下的5组数据计算得到回归直线的方程为![]() ,相关系数为
,相关系数为![]() ,相关指数为
,相关指数为![]() .以下结论中,不正确的是
.以下结论中,不正确的是
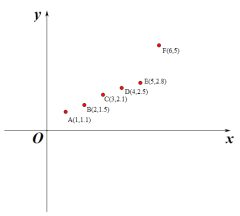
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
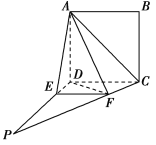
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
(1)证明:CF⊥平面ADF;
(2)求二面角DAFE的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com