
【题目】(1)解不等式![]() ≥
≥![]() 的解集.
的解集.
(2) 关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1){x|x≤-3或x≥2};(2)![]() .
.
【解析】试题分析:(1)分段去绝对值求解不等式即可
(2)由于二次项系数含有参数,故需对其进行讨论.对于二次项系数不为0时,借助于相应二次函数的特征,可建立不等式组,从而求出实数m的取值范围.
试题解析:
(1)当x<-2时,不等式等价于-(x-1)-(x+2)≥5,解得x≤-3;
当-2≤x<1时,不等式等价于-(x-1)+(x+2)≥5,即3≥5,无解;
当x≥1时,不等式等价于x-1+x+2≥5,解得x≥2.
综上,不等式的解集为{x|x≤-3或x≥2}.
(2)①当![]() ,即
,即![]() 或
或![]() 时,要使原不等式的解集为R,则
时,要使原不等式的解集为R,则![]()
②当![]() 时,要使原不等式的解集为
时,要使原不等式的解集为![]() ,则有:
,则有:
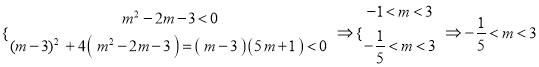
综合(1)(2)的![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
①﹣3是函数y=f(x)的极值点;
②﹣1是函数y=f(x)的最小值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(﹣3,1)上单调递增.
则正确命题的序号是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上. 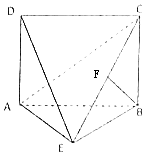
(1)求证:AE⊥BE;
(2)求三棱锥C﹣ADE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 50 | 60 | 70 |
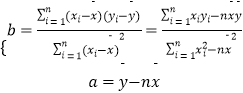
(1)画出散点图;
(2)求线性回归方程;
(3)预测当广告费支出为7百万元时的销售额.参考公式:.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com