
分析 (1)通过Sn=2an-a1与Sn-1=2an-1-a1作差可知an=2an-1(n>1),进而可知数列{an}是首项、公比均为2的等比数列,计算即得结论;
(2)通过(1)得$\frac{n}{a_n}=\frac{n}{2^n}$,进而利用错位相减法计算即得结论.
解答 解:(1)由已知Sn=2an-a1,有an=Sn-Sn-1=2an-2an-1(n>1),
即an=2an-1(n>1),从而a2=2a1,a3=4a1.
又因为a1+4是a2,a3的等差中项,即2(a1+4)=a2+a3,解得a1=2.
所以数列{an}是首项为2,公比为2的等比数列,
故${a_n}={2^n}$;
(2)由(1)得$\frac{n}{a_n}=\frac{n}{2^n}$,
所以${T_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n}{2^n}$,
$2{T_n}=1+1+\frac{3}{2^2}+…+\frac{n}{{{2^{n-1}}}}$,
两式相减${T_n}=1+\frac{1}{2}+\frac{1}{2^2}+…+\frac{1}{{{2^{n-1}}}}-\frac{n}{2^n}=\frac{{1-{{(\frac{1}{2})}^n}}}{{1-\frac{1}{2}}}-\frac{n}{2^n}=2-\frac{n+2}{2^n}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
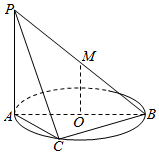 如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:
如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
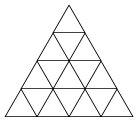 设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )
设有一个等边三角形网格,其中各个最小等边三角形的边长都是4$\sqrt{3}$cm,现用直径等于2cm的硬币投掷到此网格上,则硬币落下后与格线没有公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,∞) | B. | [1,2) | C. | (-2,-1] | D. | (-2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com