
分析 由题意画出图形,利用椭圆定义转化可得使△PAF的周长最大时的P的位置,求出其纵坐标,代入三角形面积公式得答案.
解答 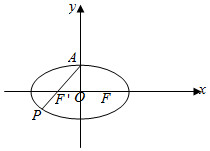 解:由椭圆$C:\frac{x^2}{2}+{y^2}=1$,得a2=2,b2=1,
解:由椭圆$C:\frac{x^2}{2}+{y^2}=1$,得a2=2,b2=1,
则c2=a2-b2=1.
∴F(1,0),而A(0,1),
如图:
设F′是左焦点,
则△APF周长=|AF|+|AP|+|PF|=|AF|+|AP|+2a-|PF′|=3a+|AP|-|PF′|
≤$3\sqrt{2}$+|AF′|(A,P,F′三点共线时,且P在AF′的延长线上,取等号),
直线AF′的方程为y=x+1,与椭圆方程联立可得${y}_{P}=-\frac{1}{3}$.
∴当△PAF的周长最大时,△PAF的面积为$\frac{1}{2}×2×(1+\frac{1}{3})=\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查椭圆的定义,以及三点共线时取得最值,同时考查三角形面积的计算,确定P的坐标是关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{25}{4}$,8] | B. | [$\frac{31}{5}$,$\frac{212}{9}$] | C. | [8,$\frac{212}{9}$] | D. | [$\frac{31}{5}$,8] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=|2x-1|+|x+1|.
已知函数f(x)=|2x-1|+|x+1|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=±\frac{1}{2}x$ | B. | y=±2x | C. | $y=±\frac{{\sqrt{5}}}{5}x$ | D. | $y=±\sqrt{5}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (1,3) | C. | (-∞,-2)∪(1,3) | D. | (-∞,-2)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{9\sqrt{3}}{8}$ | D. | $\frac{9\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com