
 已知函数f(x)=|2x-1|+|x+1|.
已知函数f(x)=|2x-1|+|x+1|.分析 (1)求出f(x)的分段函数的形式,画出函数的图象,结合图象求出不等式的解集即可;
(2)求出m的值,得到${a^2}+1+{b^2}+1=\frac{7}{2}$,根据不等式的性质证明即可.
解答 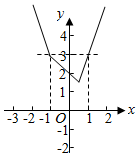 解:(1)因为f(x)=|2x-1|+|x+1|=$\left\{{\begin{array}{l}{-3x,x<-1}\\{-x+2,-1≤x≤\frac{1}{2}}\\{3x,x>\frac{1}{2}}\end{array}}\right.$,
解:(1)因为f(x)=|2x-1|+|x+1|=$\left\{{\begin{array}{l}{-3x,x<-1}\\{-x+2,-1≤x≤\frac{1}{2}}\\{3x,x>\frac{1}{2}}\end{array}}\right.$,
所以作出函数f(x)的图象如图所示.
从图中可知满足不等式f(x)≤3的解集为[-1,1].
(2)证明:从图中可知函数y=f(x)的最小值为$\frac{3}{2}$,即$m=\frac{3}{2}$.
所以${a^2}+{b^2}=\frac{3}{2}$,从而${a^2}+1+{b^2}+1=\frac{7}{2}$,
故$\frac{1}{{{a^2}+1}}+\frac{4}{{{b^2}+1}}$=$\frac{2}{7}$[(a2+1)+(b2+1)]($\frac{1}{{a}^{2}+1}$+$\frac{4}{{b}^{2}+1}$)
=$\frac{2}{7}[5+(\frac{{{b^2}+1}}{{{a^2}+1}}+\frac{{4({a^2}+1)}}{{{b^2}+1}})]≥$$\frac{2}{7}[5+2\sqrt{\frac{{{b^2}+1}}{{{a^2}+1}}•\frac{{4({a^2}+1)}}{{{b^2}+1}}}]=\frac{18}{7}$,
当且仅当$\frac{{{b^2}+1}}{{{a^2}+1}}=\frac{{4({a^2}+1)}}{{{b^2}+1}}$时,等号成立,
即${a^2}=\frac{1}{6}$,${b^2}=\frac{4}{3}$时,原式有最小值,
所以$\frac{1}{{{a^2}+1}}+\frac{4}{{{b^2}+1}}≥\frac{18}{7}$得证.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及数形结合思想,考查不等式的性质,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,2) | B. | (-3,1] | C. | [1,2) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-i | B. | 1+i | C. | -1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com