
 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.分析 (1)取AB中点M,连接MF,MC,可得四边形MFDC为平行四边形,MC∥FD;
由CM⊥AB,得DF⊥AB;又CD⊥AB,CD∩DF=D,即可得AB⊥平面CDF.
(2)异面直线BE,AD所成角即直线DA,DC所成角,可得AC=CD=2,
以B为原点,建立空间直角坐标系B-xyz,如图2所示,
则$B(0,\;\;0,\;\;0),\;\;E(4,\;\;0,\;\;0),\;\;A(0,\;\;1,\;\;\sqrt{3}),\;\;C(0,\;\;2,\;\;0),\;\;F({2,\;\;\frac{1}{2},\;\;\frac{{\sqrt{3}}}{2}})$,$\overrightarrow{BF}=({2,\;\;\;\frac{1}{2},\;\;\frac{{\sqrt{3}}}{2}}),\;\;\overrightarrow{BC}=(0,\;\;2,\;\;0)$,利用向量法求解
解答 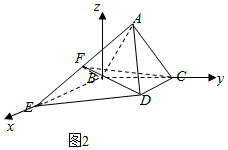 解:(1)证明:取AB中点M,连接MF,MC,因为M为AB中点,
解:(1)证明:取AB中点M,连接MF,MC,因为M为AB中点,
所以MF平行且等于$\frac{1}{2}BE$,
又CD平行且等于$\frac{1}{2}BE$,所以MF平行且等于CD,
所以四边形MFDC为平行四边形,所以MC∥FD;
因为△ABC为正三角形,M为AB中点,所以CM⊥AB,从而DF⊥AB;
又平面ABC⊥平面BCDE,CD⊥BC,平面ABC∩平面BCDE=BC,
∴CD⊥平面ABC,
∵CD⊥AB,CD∩DF=D,∴AB⊥平面CDF.
(2)解:异面直线BE,AD所成角即直线DA,DC所成角,则∠ADC=45°,
又∠ACD=90°,则AC=CD=2,
以B为原点,建立空间直角坐标系B-xyz,如图2所示,
则$B(0,\;\;0,\;\;0),\;\;E(4,\;\;0,\;\;0),\;\;A(0,\;\;1,\;\;\sqrt{3}),\;\;C(0,\;\;2,\;\;0),\;\;F({2,\;\;\frac{1}{2},\;\;\frac{{\sqrt{3}}}{2}})$,$\overrightarrow{BF}=({2,\;\;\;\frac{1}{2},\;\;\frac{{\sqrt{3}}}{2}}),\;\;\overrightarrow{BC}=(0,\;\;2,\;\;0)$,
设平面BCF的法向量为$\overrightarrow n=(x,\;\;y,\;\;z)$,
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BF}=0\\ \overrightarrow n•\overrightarrow{BC}=0,\;\;\end{array}\right.$即$\left\{\begin{array}{l}2x+\frac{1}{2}y+\frac{{\sqrt{3}}}{2}z=0,\;\;\\ 2y=0,\;\;\end{array}\right.$解得$\left\{\begin{array}{l}x=-\frac{{\sqrt{3}}}{4}z,\;\;\\ y=0,\;\;\end{array}\right.$
令z=-4,得$\vec n=(\sqrt{3},\;\;0,\;\;-4)$,
由(1)可知AB⊥平面CDF,
所以$\overrightarrow{AB}=(0,\;\;-1,\;\;-\sqrt{3})$为平面CDF的一个法向量.cos$<\overrightarrow{AB},\overrightarrow{n}>$=$\frac{\overrightarrow{AB}•\overrightarrow{n}}{|\overrightarrow{AB}||\overrightarrow{n}|}$=$\frac{4\sqrt{3}}{\sqrt{19}×2}$=$\frac{2\sqrt{57}}{19}$
∵二面角B-CF-D为钝角,所以二面角B-CF-D的余弦值为$-\frac{{2\sqrt{57}}}{19}$.
点评 本题考查了空间线面垂直的判定,向量法求二面角,考查了计算能力、空间想象能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-i | B. | 1+i | C. | -1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{21}{4}$ | B. | $\frac{21}{2}$ | C. | 42 | D. | 84 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别是A1B,AC1的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别是A1B,AC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,点P是圆O:x2+y2=1与x轴正半轴的交点,半径OA在x轴的上方,现将半径OA绕原点O逆时针旋转$\frac{π}{3}$得到半径OB.设∠POA=x(0<x<π),$f(x)=(\overrightarrow{OA}+\overrightarrow{OB})•\overrightarrow{OP}$.
如图,在平面直角坐标系xOy中,点P是圆O:x2+y2=1与x轴正半轴的交点,半径OA在x轴的上方,现将半径OA绕原点O逆时针旋转$\frac{π}{3}$得到半径OB.设∠POA=x(0<x<π),$f(x)=(\overrightarrow{OA}+\overrightarrow{OB})•\overrightarrow{OP}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com