Question

17．已知函数f（x）=|ax-1|-（a-1）x．
（i） 当a=2时，满足不等式f（x）＞0的x的取值范围为（-∞，$\frac{1}{3}$）∪（1，+∞）；
（ii） 若函数f（x）的图象与x轴没有交点，则实数a的取值范围为[$\frac{1}{2}$，1]．

Answer 1

分析 （i）化为分段函数，再解不等式即可，
（ii）①）当a≥1②当0＜a＜1③当a≤0三种情况，画出f（x）=|ax-1|与g（x）=（a-1）x的图象，利用图象确定有无交点．

解答 解：（i）当a=2时，f（x）=|2x-1|-x=$\left\{\begin{array}{l}{x-1，x≥\frac{1}{2}}\\{1-3x，x＜\frac{1}{2}}\end{array}\right.$，
∵f（x）＞0，
∴$\left\{\begin{array}{l}{x-1＞0}\\{x≥\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{1-3x＞0}\\{x＜\frac{1}{2}}\end{array}\right.$，
解得x＞1或x＜$\frac{1}{3}$，
故不等式f（x）＞0的x的取值范围为（-∞，$\frac{1}{3}$）∪（1，+∞）
（ii）函数f（x）的图象与x轴没有交点，
 ①当a≥1时，f（x）=|ax-1|与g（x）=（a-1）x的图象：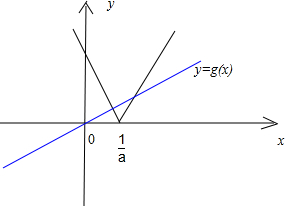

两函数的图象恒有交点，
②当0＜a＜1时，f（x）=|ax-1|与g（x）=（a-1）x的图象：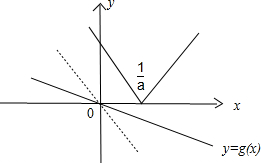

要使两个图象无交点，斜率满足：a-1≥-a，
∴a≥$\frac{1}{2}$，故$\frac{1}{2}$≤a＜1
③当a≤0时，f（x）=|ax-1|与g（x）=（a-1）x的图象：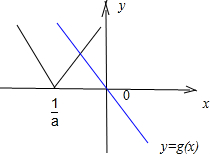

两函数的图象恒有交点，
综上①②③知：$\frac{1}{2}$≤a＜1
故答案为：.$（-∞，\frac{1}{3}）∪（1，+∞）$，$[\frac{1}{2}，1）$

点评 本题主要考查函数图象的运用，如果函数的图象能画出，结合图象解题形象而直观，属于中档题．