
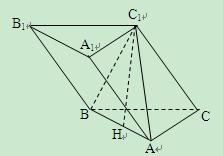
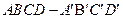 的棱长为1,点
的棱长为1,点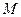 是棱
是棱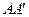 的中点,点
的中点,点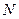 是棱
是棱 的中点,点
的中点,点 是上底面
是上底面 的中心.
的中心.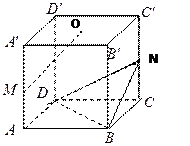 (Ⅰ)求证:MO∥平面NBD;
(Ⅰ)求证:MO∥平面NBD;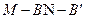 的大小;
的大小;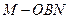 的体积.
的体积. 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
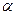 、
、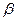 、
、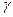 是三个不同的平面,a、b是两条不同的直线,给出下列4个命题:
是三个不同的平面,a、b是两条不同的直线,给出下列4个命题: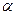 ,b∥
,b∥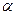 ,则a∥b; ②若a∥
,则a∥b; ②若a∥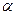 ,b∥
,b∥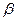 ,a∥b,则
,a∥b,则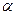 ∥
∥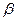 ;③若a⊥
;③若a⊥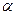 ,b⊥
,b⊥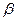 ,a⊥b,则
,a⊥b,则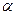 ⊥
⊥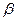 ;④若a、b在平面
;④若a、b在平面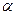 内的射影互相垂直,则a⊥b. 其中正确命题是( )
内的射影互相垂直,则a⊥b. 其中正确命题是( )| A.③ | B.④ | C.①③ | D.②④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
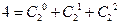 ,
,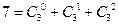 ,
,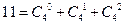 ;……
;……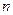 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分(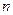 >1)?证明你的结论;
>1)?证明你的结论;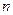 个平面最多将空间分割成多少个部分(
个平面最多将空间分割成多少个部分(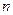 >2)?证明你的结论
>2)?证明你的结论查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com