
���� ��1����$\frac{1}{2}$kx-$\frac{1}{80}$��1+k2��x2=0�ã�x=$\frac{40k}{1+{k}^{2}}$��x=0�����û�������ʽ�������������̣�
��2�����$\frac{1}{2}��k��\frac{9}{2}$�������⣺$\frac{1}{2}$ka-$\frac{1}{80}$��1+k2��a2=2.55�ڣ�$\frac{1}{2}$��$\frac{9}{2}$������ʵ���⣬���ɵó����ۣ�
��� �⣺��1����$\frac{1}{2}$kx-$\frac{1}{80}$��1+k2��x2=0�ã�x=$\frac{40k}{1+{k}^{2}}$��x=0������2�֣�
��x=$\frac{40}{k+\frac{1}{k}}$��20�����ҽ���k=1ʱȡ�Ⱥţ�
��ˣ�������Ϊ20�ף� ����5�֣�
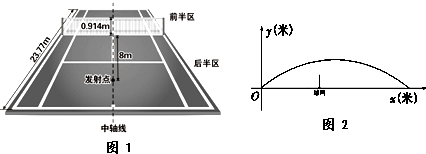
��2����������������x=8ʱy��1��
����4k-$\frac{4}{5}$��1+k2����1����4k2-20k+9��0�����$\frac{1}{2}��k��\frac{9}{2}$ ����8�֣�
�����⣺����k�ķ���$\frac{1}{2}$ka-$\frac{1}{80}$��1+k2��a2=2.55�ڣ�$\frac{1}{2}$��$\frac{9}{2}$������ʵ����
��a2k2-40ak+a2+204=0��a��0����9��
��=1600a2-4a2��a2+204����0��a��14������11�֣�
��ʱk=$\frac{10}{7}$��������ˣ����Ի����ĺ����� a���Ϊ14 ����12�֣�
���� ���⿼��������ѧ֪ʶ���ʵ�����⣬�����������ʽ�����ã�����ѧ���ļ�����������ȷת���ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 122 | B�� | 5 | C�� | 26 | D�� | 121 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 60�� | C�� | 120�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ԲC��$\frac{x^2}{2}+{y^2}$=1����֪A��1��0����B��2��0��������B��ֱ������Բ����P��Q���㣮
��ԲC��$\frac{x^2}{2}+{y^2}$=1����֪A��1��0����B��2��0��������B��ֱ������Բ����P��Q���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��0} | B�� | {-1��1} | C�� | {0��1} | D�� | {-1��0��1} |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com