
| A�� | f��x���ڣ�0��1����ǡ��һ����� | B�� | f��x���ڣ�0��1����ǡ��������� | ||
| C�� | f��x���ڣ�-1��0����ǡ��һ����� | D�� | f��x���ڣ�-1��0����ǡ��������� |
���� ���f��x���ĵ���������x��1ʱ�������ķ��ţ��жϵ����ԣ�����f��0����f��1����f��-1�����ɵ÷��ţ��������ڶ��������ɵõ����ۣ�
��� �⣺����f��x��=1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$-��+$\frac{{x}^{2013}}{2013}$-$\frac{{x}^{2014}}{2014}$+$\frac{{x}^{2015}}{2015}$��
�ɵ�f�䣨x��=1-x+x2-x3+��+x2012-x2013+x2014
=��1-x��+x2��1-x��+��+x2012��1-x��+x2014
=��1-x����1+x2+��+x2012��+x2014��
��x��1ʱ��1-x��0��f�䣨x����0��
�ɵ�f��x���ڣ�-�ޣ�1���ϵ�����
��f��0��=1��0���ɵ�f��1����0������f��x���ڣ�0��1������㣬��A��B������
��f��-1��=1-1-$\frac{1}{2}$-$\frac{1}{3}$-��-$\frac{1}{2015}$��0����f��x���ڣ�-1��0��������
�������ڶ������ɵ�f��x���ڣ�-1��0����ǡ��һ����㣮
��C��ȷ��D����
��ѡ��C��
���� ���⿼�麯�����������Ľⷨ��ע�����õ����жϵ����ԣ����ú��������ڶ��������������������ж������������е��⣮


 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��c��b | B�� | b��a��c | C�� | c��a��b | D�� | a��b��c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16�� | B�� | 64�� | C�� | 124�� | D�� | 156�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $1-\frac{{\sqrt{3}}}{2}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
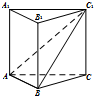 ��ͼ��������ABC-A1B1C1�ĸ����ⳤ��Ϊ2���Ҳ��ⴹֱ�ڵ��棬������C1-AB-C������ֵΪ$\frac{2\sqrt{3}}{3}$��
��ͼ��������ABC-A1B1C1�ĸ����ⳤ��Ϊ2���Ҳ��ⴹֱ�ڵ��棬������C1-AB-C������ֵΪ$\frac{2\sqrt{3}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com