
宇宙深处有一颗美丽的行星,这个行星是一个半径为r(r>0)的球。人们在行星表面建立了与地球表面同样的经纬度系统。已知行星表面上的A点落在北纬60°,东经30°;B点落在东经30°的赤道上;C点落在北纬60°,东经90°。在赤道上有点P满足PB两点间的球面距离等于AB两点间的球面距离。
(1)求AC两点间的球面距离;
(2)求P点的经度;
(3)求AP两点间的球面距离。
解析试题分析:(1)根据纬度、经度的定义求出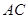 的长,在由余弦定理求
的长,在由余弦定理求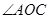 的大小,然后用弧长公式
的大小,然后用弧长公式
求AC两点间的球面距离,(2)由球面距离定义知∠POB=∠AOB=60°,又P点在赤道上,根据经度的定义可确定P点的经度;(3)连接 A,
A, C,
C,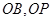 ,可知
,可知 A平行OB且等于OB的一半,延长BA与
A平行OB且等于OB的一半,延长BA与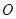
 交于D点,那么
交于D点,那么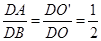 ,同理可证
,同理可证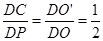 ,即四边形
,即四边形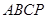 为等腰梯形,求出
为等腰梯形,求出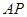 的长,然后解三角形
的长,然后解三角形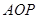 可得
可得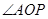 的大小。
的大小。
试题解析:设球心为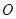 ,北纬60°圈所对应的圆心为
,北纬60°圈所对应的圆心为 ,
,
(1)那么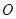
 =
=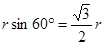 。
。 A=
A= C=
C= 。又因为∠A
。又因为∠A C=60°。
C=60°。
所以AC= 。那么由余弦定理得
。那么由余弦定理得
 ,则AC两点间的球面距离为
,则AC两点间的球面距离为 。
。
(2)PB两点间的球面距离等于AB两点间的球面距离,所以PB=AB。
可知∠POB=∠AOB=60°,又P点在赤道上,所以P点的经度为东经90°或西经30°。
显然P点的两种可能对应的AP间的球面距离相等。不妨P所在的经度为东经90°。
由条件可知 A平行OB且等于OB的一半,延长BA与
A平行OB且等于OB的一半,延长BA与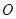
 交于D点,那么
交于D点,那么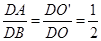 。
。
而 C平行OP且等于OP的一半,所以D、P、C共线且
C平行OP且等于OP的一半,所以D、P、C共线且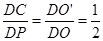 。
。
可知AC∥BP,所以A、B、C、P共面。
又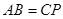 ,所以四边形
,所以四边形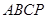 为等腰梯形,
为等腰梯形,
所以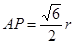 ,
,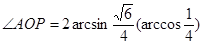 ,
,
所以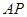 两点之间的球面距离为
两点之间的球面距离为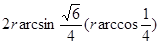
考点:(1)纬(经)的定义;(2)球面距离的定义与求法;(3)余弦定理的应用;(4)反三角函数的应用。


科目:高中数学 来源: 题型:解答题
已知正△ABC的边长为 , CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
, CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
(1)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(2)若棱锥E-DFC的体积为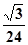 ,求
,求 的值;
的值;
(3)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出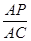 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.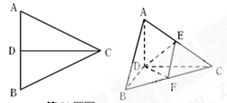
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=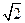 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.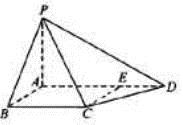
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com