
【题目】已知函数![]() (
(![]() 是常数且
是常数且![]() ),对于下列命题:
),对于下列命题:
①函数![]() 的最小值是
的最小值是![]() ;
;
②函数![]() 在
在![]() 上是单调函数;
上是单调函数;
③若![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 的取值范围是
的取值范围是![]() ;
;
④对任意的![]() 且
且![]() ,恒有
,恒有![]()
其中正确命题的序号是__________.
【答案】①③④
【解析】函数![]() (
(![]() 是常数且
是常数且![]() )的图象如图所示:
)的图象如图所示:
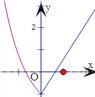
对于①,由图可得:当![]() 时,函数
时,函数![]() 的最小值是
的最小值是![]() -1;故正确;对于②,由图象说明函数
-1;故正确;对于②,由图象说明函数![]() 在
在![]() 上不是单调函数;故错误;③若
上不是单调函数;故错误;③若![]() 在
在![]() 上恒成立,则
上恒成立,则![]() ,求得
,求得![]() 的取值范围是
的取值范围是![]() ,故正确;对于④,已知函数在
,故正确;对于④,已知函数在![]() 上的图象在
上的图象在![]() 上是下凹的,所以任取两点连线应在图象的上方,即
上是下凹的,所以任取两点连线应在图象的上方,即![]() ,故正确.
,故正确.
故答案为①③④
【点晴】本题通过对多个命题真假的判断综合考查最值、单调性、恒成立问题以及数学化归思想,属于难题.该题型往往出现在在填空题最后两题,综合性较强,同学们往往因为某一点知识掌握不牢就导致本题“全盘皆输”,解答这类问题首先不能慌乱更不能因贪快而审题不清,其次先从最有把握的命题入手,最后集中力量攻坚最不好理解的命题.


科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA= ![]() acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,分别求a和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的各项都是正数,且对任意n∈N* , 都有(an﹣1)(an+3)=4Sn , 其中Sn为数列{an}的前n项和.
(1)求证数列{an}是等差数列;
(2)若数列{ ![]() }的前n项和为Tn , 求Tn .
}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|logax|(0<a<1)的定义域为[m,n](m<n),值域为[0,1],若n﹣m的最小值为![]() , 则实数a的值为( )
, 则实数a的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.
(1)在正方形内任取一点M,求事件“|AM|≤1”的概率;
(2)用大豆将正方形均匀铺满,经清点,发现大豆一共28粒,其中有22粒落在圆中阴影部分内,请据此估计圆周率π的近似值(精确到0.01). 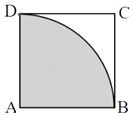
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com