
分析 (1)由anan+1=a1a1qn-1=rqn-1,anan+1+an+1an+2>an+2an+3,知rqn-1+rqn>rqn+1+q>q2 即:q2-q-1<0,可得q的取值范围;
(2)由数列{anan+1}是公比为q的等比数列,知$\frac{{a}_{n+1}{a}_{n+2}}{{a}_{n}{a}_{n+1}}$=$\frac{{a}_{n+2}}{{a}_{n}}$=q,由此能求出bn=qn-1+rqn-1=(1+r)qn-1.
(3)由bn=(1+r)qn-1,知$\frac{lo{g}_{2}{b}_{n+1}}{lo{g}_{2}{b}_{n}}$=1+$\frac{1}{n-20.2}$,由此能求出数列{$\frac{lo{g}_{2}{b}_{n+1}}{lo{g}_{2}{b}_{n}}$}的最大值和最小值.
解答 解:(1)∵数列{an}满足条件:a1=1,a2=r,
且数列{anan+1}是公比为q的等比数列,
∴q≠0,r≠0,且anan+1=a1a1qn-1=rqn-1,
∵anan+1+an+1an+2>an+2an+3,
∴rqn-1+rqn>rqn+1+q>q2
即:q2-q-1<0,
∵q>0,
∴0<q<$\frac{1+\sqrt{5}}{2}$.
(2)∵数列{anan+1}是公比为q的等比数列,
∴$\frac{{a}_{n+1}{a}_{n+2}}{{a}_{n}{a}_{n+1}}$=$\frac{{a}_{n+2}}{{a}_{n}}$=q,
∵a1=1,
∴当n=2k-1时,an=qk-1
∵a2=r,
∴当n=2k时,an=rqk-1.
∵bn=a2n-1+a2n(n∈N),
∴bn=qn-1+rqn-1=(1+r)qn-1.
(3)∵bn=(1+r)qn-1,
∴$\frac{lo{g}_{2}{b}_{n+1}}{lo{g}_{2}{b}_{n}}$=1+$\frac{1}{n-20.2}$,
记Cn=$\frac{lo{g}_{2}{b}_{n+1}}{lo{g}_{2}{b}_{n}}$,
当n-20.2>0,即n>21,n∈N+时,Cn随n的增大而减小,
∴1<Cn≤C21=$\frac{9}{4}$.
当n-20.2<0,即n≤20,n∈N+时,Cn随n的增大而减小,
∴1>Cn≥C20=-4.
综上所述,对任意的自然数n,有C20≤Cn≤C21,
∴数列{$\frac{lo{g}_{2}{b}_{n+1}}{lo{g}_{2}{b}_{n}}$}中,n=21时,取最大值,n=20时,取最小值-4
点评 本题考查数列的综合应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.


科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(文)试卷(解析版) 题型:选择题
已知函数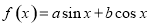 (
( 为常数,
为常数, ,
, )在
)在 处取得最大值,则函数
处取得最大值,则函数 是( )
是( )
A.奇函数且它的图象关于点 对称
对称
B.奇函数且它的图象关于点 对称
对称
C.偶函数且它的图象关于点 对称
对称
D.偶函数且它的图象关于点 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,为了测定对岸A、B两点之间的距离,在河的一岸定一条基线CD,测得CD=100米,∠ACD=80°,∠BCD=45°,∠BDC=70°,∠ADC=33°,求A、B间的距离.
如图,为了测定对岸A、B两点之间的距离,在河的一岸定一条基线CD,测得CD=100米,∠ACD=80°,∠BCD=45°,∠BDC=70°,∠ADC=33°,求A、B间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,点A(x1,y1)、B(x2,y2)在单位圆上,∠xOA=α,∠AOB=$\frac{π}{3}$,且α∈($\frac{π}{6}$,$\frac{π}{3}$).
如图,在平面直角坐标系xOy中,点A(x1,y1)、B(x2,y2)在单位圆上,∠xOA=α,∠AOB=$\frac{π}{3}$,且α∈($\frac{π}{6}$,$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {1,5} | C. | {2,4} | D. | {1,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com