
【题目】已知抛物线![]() ,
,![]() 、
、![]() 、
、![]() 为抛物线
为抛物线![]() 上不同的三点.
上不同的三点.
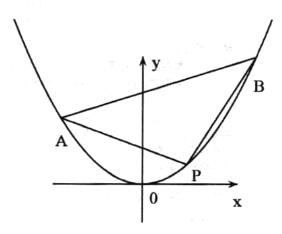
(1)当点![]() 的坐标为
的坐标为![]() 时,若直线
时,若直线![]() 过抛物线焦点
过抛物线焦点![]() 且斜率为
且斜率为![]() ,求直线
,求直线![]() 、
、![]() 斜率之积;
斜率之积;
(2)若![]() 为以
为以![]() 为顶点的等腰直角三角形,求
为顶点的等腰直角三角形,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设点![]() 、
、![]() ,可得出直线
,可得出直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与抛物线的方程联立,列出韦达定理,然后利用斜率公式结合韦达定理可计算出直线
的方程与抛物线的方程联立,列出韦达定理,然后利用斜率公式结合韦达定理可计算出直线![]() 、
、![]() 斜率之积;
斜率之积;
(2)设点![]() 、
、![]() 、
、![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,不妨设
,不妨设![]() ,可得出直线
,可得出直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,求出
的方程联立,求出![]() ,同理得出
,同理得出![]() ,再由
,再由![]() 得出
得出![]() ,然后利用三角形的面积公式,结合基本不等式求出
,然后利用三角形的面积公式,结合基本不等式求出![]() 面积的最小值.
面积的最小值.
(1)设点![]() 、
、![]() ,则
,则 ,
,
直线![]() 的斜率为
的斜率为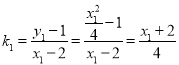 ,同理,直线
,同理,直线![]() 的斜率为
的斜率为![]() .
.
抛物线![]() 的焦点为
的焦点为![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,且过点
,且过点![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立
的方程联立 ,得
,得![]() ,
,
![]() ,由韦达定理得
,由韦达定理得![]() ,
,![]() .
.
因此,直线![]() 、
、![]() 斜率之积为
斜率之积为![]() ;
;
(2)设点![]() 、
、![]() 、
、![]() ,
,
设直线![]() 的斜率为
的斜率为![]() ,不妨设
,不妨设![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
联立直线![]() 与抛物线
与抛物线![]() 的方程
的方程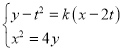 ,消去
,消去![]() 得
得![]() ,
,
由韦达定理得![]() ,
,![]() ,
,![]() ,同理可得
,同理可得![]() ,
,
![]() ,同理可得
,同理可得![]() ,
,
由题中图象可知,![]() 与
与![]() 符号相反,
符号相反,
由![]() 得
得![]() ,则
,则![]() ,
,
化简得![]() ,
,
故![]() 的面积为
的面积为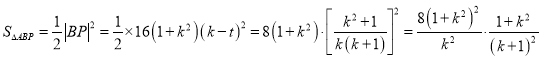
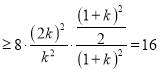 ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
因此,![]() 面积的最小值为
面积的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.

给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上恰有两个不同的零点,求实数a的取值范围;
在定义域上恰有两个不同的零点,求实数a的取值范围;
(3)设函数![]() 在区间
在区间![]() )上存在极值,求证:
)上存在极值,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,同比增长率一般是指和去年同期相比较的增长率,环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表,根据2019年居民消费价格月度涨跌幅度统计折线图,下列说法正确的是( )
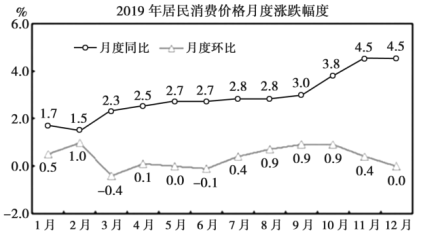
A.2019年我国居民每月消费价格与2018年同期相比有涨有跌
B.2019年我国居民每月消费价格中2月消费价格最高
C.2019年我国居民每月消费价格逐月递增
D.2019年我国居民每月消费价格3月份较2月份有所下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.


![]()
![]()
(1)已知抽取的100个使用A款订餐软件的商家中,甲商家的“平均送达时间”为18分钟。现从使用A款订餐软件的商家中“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以昆明、玉溪为中心的滇中地区,冬无严寒、夏无酷暑,世界上主要的鲜切花品种在这里都能实现周年规模化生产.某鲜花批发店每天早晨以每支2元的价格从鲜切花生产基地购入某种玫瑰,经过保鲜加工后全部装箱(每箱500支,平均每支玫瑰的保鲜加工成本为1元),然后以每箱2000元的价格整箱出售.由于鲜花的保鲜特点,制定了如下促销策略:若每天下午3点以前所购进的玫瑰没有售完,则对未售出的玫瑰以每箱1200元的价格降价处理.根据经验,降价后能够把剩余玫瑰全部处理完毕,且当天不再购进该种玫瑰,由于库房限制每天最多加工6箱.
(1)若某天该鲜花批发店购入并加工了6箱该种玫瑰,在下午3点以前售出4箱,且被6位不同的顾客购买.现从这6位顾客中随机选取2人赠送优惠卡,则恰好一位是以2000元价格购买的顾客,另一位是以1200元价格购买的顾客的概率是多少?
(2)该鲜花批发店统计了100天内该种玫瑰在每天下午3点以前的销售量![]() (单位:箱),统计结果如下表所示(视频率为概率):
(单位:箱),统计结果如下表所示(视频率为概率):
| 4 | 5 | 6 |
频数 | 30 |
|
|
①估计接下来的一个月(30天)内该种玫瑰每天下午3点以前的销售量不少于5箱的天数是多少?
②若批发店每天在购进5箱数量的玫瑰时所获得的平均利润最大(不考虑其他成本),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com