
| A. | (-∞,3] | B. | [11,+∞) | C. | (3,11) | D. | [3,11] |
分析 要使原式恒成立,只需 m2-14m≤f(x)min,然后再利用导数求函数f(x)=-x3-2x2+4x,当x∈[-3,3]的最值即可.
解答 解:因为f(x)=-x3-2x2+4x,当x∈[-3,3]
所以f′(x)=-3x2-4x+4,令f′(x)=0得x=$\frac{2}{3}$或x=-2,
因为该函数在闭区间[-3,3]上连续可导,且极值点处的导数为零,
所以最小值一定在端点处或极值点处取得,
而f(-3)=-3,f(-2)=-8,f($\frac{2}{3}$)=$\frac{40}{27}$,f(3)=-33,
所以该函数的最小值为-33,
因为f(x)≥m2-14m恒成立,
只需m2-14m≤f(x)min,
即m2-14m≤-33,即m2-14m+33≤0
解得3≤m≤11.
故选:D.
点评 本题考查了不等式恒成立问题,一般是转化为函数的最值问题来解决,而本题涉及到了可导函数在闭区间上的最值问题,因此我们只是从端点值和极值中找最值,而极值点处导数为零,因此最终是从导数为零、端点值中找的最值.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{30}}{6}$ | B. | $\sqrt{7}$ | C. | $\frac{\sqrt{30}}{6}$或$\sqrt{7}$ | D. | $\frac{5}{6}$或7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
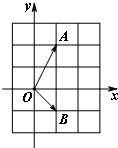
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com