
分析 (1)利用反证法,即可证明.
(2)根据题意,问题转化为“存在b∈[0,1],使f(b)=f-1(b)”,即y=f(x)的图象与函数y=f-1(x)的图象有交点,且交点的横坐标b∈[0,1].由y=f(x)的图象与y=f-1(x)的图象关于直线y=x对称,得到函数y=f(x)的图象与y=x有交点,且交点横坐标b∈[0,1].因此,将方程化简整理得ex=x2-x+a,记F(x)=ex,G(x)=x2-x+a,由零点存在性定理建立关于a的不等式组,解之即可得到实数a的取值范围.
解答 解:(1)假设f(b)≠b,则f(b)>b或f(b)<b,
∵f(x)=$\sqrt{{e}^{x}+x-a}$,(a∈R,e为自然对数的底数).在其定义域为增函数,
∴f(f(b))>f(b)或f(f(b))<b,
这与f(f(b))=b成立相矛盾,
故假设不成立,
∴f(b)=b;
(2)由f(f(b))=b,可得f(b)=f-1(b)
其中f-1(x)是函数f(x)的反函数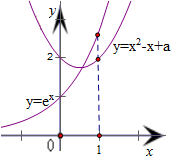
因此命题“存在b∈[0,1]使f(f(b))=b成立”,转化为
“存在b∈[0,1],使f(b)=f-1(b)”,
即y=f(x)的图象与函数y=f-1(x)的图象有交点,
且交点的横坐标b∈[0,1],
∵y=f(x)的图象与y=f-1(x)的图象关于直线y=x对称,
∴y=f(x)的图象与函数y=f-1(x)的图象的交点必定在直线y=x上,
由此可得,y=f(x)的图象与直线y=x有交点,且交点横坐标b∈[0,1],
根据$\sqrt{{e}^{x}+x-a}$=x,化简整理得ex=x2-x+a
记F(x)=ex,G(x)=x2-x+a,在同一坐标系内作出它们的图象,
可得$\left\{\begin{array}{l}{F(0)≤G(0)}\\{F(1)≥G(1)}\end{array}\right.$,即$\left\{\begin{array}{l}{{e}^{0}<{0}^{2}-0+a}\\{e>1-1+a}\end{array}\right.$,解之得1≤a≤e
即实数a的取值范围为[1,e]
故选:A
点评 本题给出含有根号与指数式的基本初等函数,在存在b∈[0,1]使f(f(b))=b成立的情况下,求参数a的取值范围.着重考查了基本初等函数的图象与性质、函数的零点存在性定理和互为反函数的两个函数的图象特征等知识,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
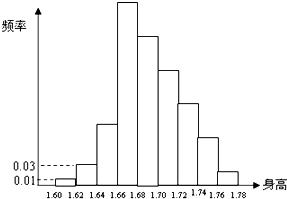 为了解某校身高在1.60m~1.78m的高一学生的情况,随机地抽查了该校200名高一学生,得到如图1所示频率直方图.由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为m,身高在1.66m~1.74m的学生数为n,则m,n的值分别为( )
为了解某校身高在1.60m~1.78m的高一学生的情况,随机地抽查了该校200名高一学生,得到如图1所示频率直方图.由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为m,身高在1.66m~1.74m的学生数为n,则m,n的值分别为( )| A. | 0.27,78 | B. | 0.27,156 | C. | 0.81,78 | D. | 0.09,83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com