
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 与
与![]() 的交点为
的交点为![]() .
.
(1)判断点![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)点![]() 为曲线
为曲线![]() 上的任意一点,求
上的任意一点,求![]() 的最大值.
的最大值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先联立两直线的极坐标方程,求出交点的极坐标,再利用互化公式得到交点的直角坐标,消参得到曲线的普通方程,代点判定点和曲线的位置关系;(2)利用两点间的距离公式和二次函数的最值进行求解.
试题解析:(1)法一:由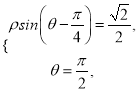 得
得![]() ,
,
所以![]() 与
与![]() 的交点
的交点![]() 的极坐标为
的极坐标为![]() ,即点
,即点![]() 的直角坐标为
的直角坐标为![]() .
.
又曲线C的普通方程为![]() ,
,
且![]() ,所以点M在曲线
,所以点M在曲线![]() 上.
上.
法二:直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
由![]() 得
得![]() 所以
所以![]() 与
与![]() 的交点
的交点![]() 的直角坐标为
的直角坐标为![]() .
.
又曲线C的普通方程为![]() ,且
,且![]() ,所以点M在曲线
,所以点M在曲线![]() 上.
上.
(2)法一:设点P的直角坐标为![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.
法二:设点P![]() ,其中
,其中![]() ,
,
则![]() ,
,
所以当![]() 时,
时, ![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,小波从![]() 街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是
街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是![]() ,红灯亮的概率都是
,红灯亮的概率都是![]() .
.
(1)求小波遇到4次绿灯后,处于![]() 街区的概率;
街区的概率;
(2)若小波一共遇到了3次红绿灯,设此时小波所处的街区与![]() 街区相距的街道数为
街区相距的街道数为![]() (如小波若处在
(如小波若处在![]() 街区则相距零个街道,处在
街区则相距零个街道,处在![]() ,
,![]() 街区都是相距2个街道),求
街区都是相距2个街道),求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一名学生每天骑车上学,从他家里到学校的途中有6个交通岗,假设在每个交通岗遇到红灯的事件是相互独立的,并且概率都是![]() .
.
(1)假设![]() 为这名学生在途中遇到红灯的次数,求
为这名学生在途中遇到红灯的次数,求![]() 的分布列;
的分布列;
(2)设![]() 为这名学生在首次停车前经过的路口数,求
为这名学生在首次停车前经过的路口数,求![]() 的分布列;
的分布列;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下:

试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在[70,80)之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80),[80,90)和[90,100]分数段的试卷中抽取8份进行分析,再从中任选3人进行交流,求交流的学生中,成绩位于[70,80)分数段的人数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了300名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 180 | ||
女大学生 | 45 | ||
合计 | 200 |
(Ⅰ)根据题意完成表格;
(Ⅱ)是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
附:![]() ,
,![]()
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | .072 | 2.706 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
Ⅰ.请完成上面的列联表;
Ⅱ.根据列联表的数据,是否有![]() 的把握认为“成绩与班级有关系”.
的把握认为“成绩与班级有关系”.
参考公式与临界值表:![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() .
.
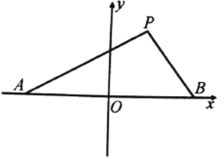
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为
的轨迹为![]() ,点
,点![]() 是轨迹为
是轨迹为![]() 上不同于
上不同于![]() 的两点,且满足
的两点,且满足![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com