
分析 (1)设甲同学选中C课程为事件A,乙同学选中C课程为事件B,丙同学选中C课程为事件C,甲同学选中C课程且乙、丙同学未选C课程为事件D,由P(D)=P(A)P($\overline{B}$)P($\overline{C}$),能求出甲同学选中C课程且乙、丙同学未选C课程的概率.
(2)由题意得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望E(X).
解答 解:(1)设甲同学选中C课程为事件A,乙同学选中C课程为事件B,丙同学选中C课程为事件C,
甲同学选中C课程且乙、丙同学未选C课程为事件D,
由P(A)=$\frac{{C}_{2}^{1}}{{C}_{3}^{2}}$=$\frac{2}{3}$,P($\overline{B}$)=$\frac{{C}_{4}^{3}}{{C}_{5}^{3}}$=$\frac{2}{5}$,P($\overline{C}$)=$\frac{{C}_{4}^{3}}{{C}_{5}^{3}}$=$\frac{2}{5}$,
由题意知每位同学选课彼此独立,
∴甲同学选中C课程且乙、丙同学未选C课程的概率:
P(D)=P(A)P($\overline{B}$)P($\overline{C}$)=$\frac{2}{3}×\frac{2}{5}×\frac{2}{5}$=$\frac{8}{75}$.
(2)由题意得X的可能取值为0,1,2,3,
P(X=0)=$\frac{1}{3}×\frac{2}{5}×\frac{2}{5}$=$\frac{4}{75}$,
P(X=1)=$\frac{2}{3}×\frac{2}{5}×\frac{2}{5}$+$\frac{1}{3}×\frac{3}{5}×\frac{2}{5}$+$\frac{1}{3}×\frac{2}{5}×\frac{3}{5}$=$\frac{20}{75}$,
P(X=2)=$\frac{2}{3}×\frac{3}{5}×\frac{2}{5}+\frac{2}{3}×\frac{2}{5}×\frac{3}{5}$+$\frac{1}{3}×\frac{3}{5}×\frac{3}{5}$=$\frac{33}{75}$,
P(X=3)=$\frac{2}{3}×\frac{3}{5}×\frac{3}{5}$=$\frac{18}{75}$.
则X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{4}{75}$ | $\frac{4}{15}$ | $\frac{11}{25}$ | $\frac{6}{25}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| A | 甲 | 4次 | 6次 | 2次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 综合得分k的取值范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
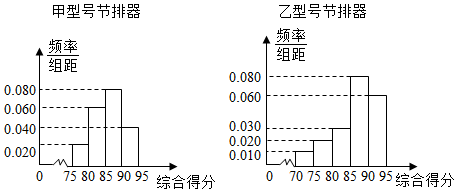
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [10,25) | [25,40) | [40,55] |
| 成绩优秀 | 670 | a | b |
| 成绩一般 | 80 | 60 | c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com