Question

8．P，Q为椭圆上的任意两点，延长PQ交焦点F所对应的准线于点R，求证：FR为∠PFQ的外角平分线．

Answer 1

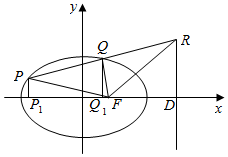
分析 可设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），右焦点F（c，0），右准线为l：x=$\frac{{a}^{2}}{c}$，过P，Q向准线分别作垂线PP₁，QQ₁交准线于P₁，Q₁，由椭圆的第二定义，结合平行线分线段成比例，以及外角平分线的判定定理，即可得证．

解答 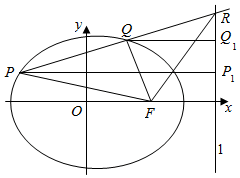证明：可设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），
右焦点F（c，0），右准线为l：x=$\frac{{a}^{2}}{c}$，
过P，Q向准线分别作垂线PP₁，QQ₁交准线于P₁，Q₁，
由椭圆的第二定义，可得e=$\frac{PF}{P{P}_{1}}$=$\frac{QF}{Q{Q}_{1}}$，
即有$\frac{QF}{PF}$=$\frac{Q{Q}_{1}}{P{P}_{1}}$，
又QQ₁∥PP₁，可得
$\frac{Q{Q}_{1}}{P{P}_{1}}$=$\frac{QR}{PR}$，
即有$\frac{QF}{PF}$=$\frac{QR}{PR}$，
由外角平分线的判定定理，
可得FR为∠PFQ的外角平分线．

点评 本题考查椭圆的定义、方程和性质，考查定义法的运用，以及平行线分线段成比例，同时考查外角平分线的判定定理，属于中档题．