
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
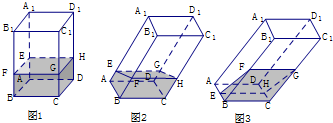
分析 由题意抓住棱柱形的特征进行判断,观察即可得到答案.
解答 解:∵棱柱特征:有两个面是相互平行且是全等的多边形,
其余梅相邻两个面的交线也相互平行,而这些面都是平行四边形
∴通过棱柱特征,①②正确.
∵水面EFGH所在四边形的面积,
从图2,图3我们发现,有条边长不变,而另外一条长随倾斜度变化而变化,∴EFGH所在四边形的面积是变化的.③不对
∵棱A1D1 始终与BC平行,BC与水面始终平行,∴④正确.
∵水的体积是不变的,高始终是BC也不变.底面也不会,即BE•BF是定值.
∴⑤正确.
所以正确的是:①②④⑤.
故选C.
点评 本题考查了棱柱特征:有两个面是相互平行且是全等的多边形,其余梅相邻两个面的交线也相互平行,而这些面都是平行四边形,同时考查对空间的想象力和图象变形的灵活处理能力.属于中档题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:选择题
| A. | an=2n-3 | B. | an=2n-4 | C. | an=3-3n | D. | an=2n-5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
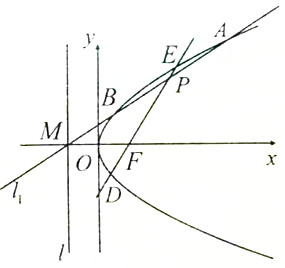 已知抛物线C:y2=2px(p>0)的焦点F与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点重合,抛物线C的准线l与x轴的交点为M,过点M且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF与抛物线C交于D,E两点
已知抛物线C:y2=2px(p>0)的焦点F与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点重合,抛物线C的准线l与x轴的交点为M,过点M且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF与抛物线C交于D,E两点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com