
 如图所示,某村在P处有一堆肥,今要把此堆肥料沿道路PA或PB送到成矩形的一块田ABCD中去,已知PA=100m,BP=120m,BC=60m,∠APB=60°,能否在田中确定一条界线,使位于界线一侧的点沿道路PA送肥较近而另一侧的点则沿PB送肥较近?如果能,请说出这条界线是什么曲线,并求出它的方程.
如图所示,某村在P处有一堆肥,今要把此堆肥料沿道路PA或PB送到成矩形的一块田ABCD中去,已知PA=100m,BP=120m,BC=60m,∠APB=60°,能否在田中确定一条界线,使位于界线一侧的点沿道路PA送肥较近而另一侧的点则沿PB送肥较近?如果能,请说出这条界线是什么曲线,并求出它的方程.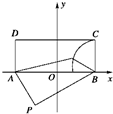 解:田地ABCD中的点可分为三类:第一类沿PA送肥近,第二类沿PB送肥较近,第三类沿PA或PB送肥一样近,由题意知,界线是第三类点的轨迹.
解:田地ABCD中的点可分为三类:第一类沿PA送肥近,第二类沿PB送肥较近,第三类沿PA或PB送肥一样近,由题意知,界线是第三类点的轨迹.| 1002+1202-2•100•120•cos60° |
| 31 |
| 31 |
| x2 |
| 100 |
| y2 |
| 3000 |


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| GA |
| PF1 |
| A、3 | B、2 |
| C、4 | D、与λ的取值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| a2n |
| 7 |
| 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| lnx |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4x |
| 4x+2 |
| 1 |
| 4011 |
| 2 |
| 4011 |
| 3 |
| 4011 |
| 4010 |
| 4011 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com