
分析 (1)由椭圆的方程,求得椭圆方程坐标,求得双曲线的焦点坐标,即c=2,由渐近线方程为y=±$\frac{4}{3}$x,则a=3λ,b=4λ,代入a2+b2=c2,求得λ=1,即可求得a和b,即可求得双曲线C的标准方程;
(2)设P(x0,y0),由PF1的中点在y轴上,知x0=5,代入即可求得y0=±$\frac{16}{3}$,则${S}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}$•丨F1F2丨•丨y0丨,即可求得△PF1F2的面积.
解答 解:(1)椭圆$\frac{{x}^{2}}{35}$+$\frac{{y}^{2}}{10}$=1的焦点为:(±5,0)…(1分)
∴双曲线的焦点为:(±5,0),
设双曲线方程:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$,
∴c=2…(3分)
双曲线的渐近线方程为y=±$\frac{4}{3}$x,
不妨设a=3λ,b=4λ(λ>0),
∵a2+b2=c2,
∴λ=1…(5分)
∴双曲线方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$…(7分)
(2)设P(x0,y0),又F1(-5,0),
由PF1的中点在y轴上,知x0=5…(9分)
代入双曲线方程,得y0=±$\frac{16}{3}$…(12分)
∴${S}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}$•丨F1F2丨•丨y0丨=$\frac{1}{2}$×10×$\frac{16}{3}$=$\frac{80}{3}$.
△PF1F2的面积为$\frac{80}{3}$.…(14分)
点评 本题考查椭圆及双曲线的标准方程及简单性质,考查三角形的面积公式,考查计算能力,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<3 | B. | 1<a<3 | C. | 2<a<3 | D. | 2≤a<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=|x| | B. | y=3-x | C. | y=$\frac{1}{x}$ | D. | y=-x2+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(文)试卷(解析版) 题型:解答题
某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段,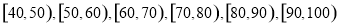 进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
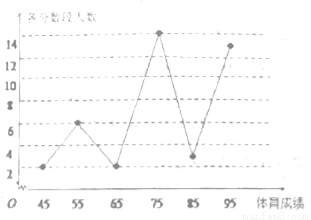
(1)体育成绩大于或等于70分的学生常被称为“体育良好”,已知该校高一年级有1000名学生,试估计高一年级中“体育良好”的学生人数;
(2)为分析学生平时的体育活动情况,现从体育成绩在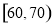 和
和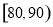 的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在
的样本学生中随机抽取2人,求在抽取的2名学生中,至少有1人体育成绩在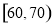 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com