
根据空气质量指数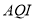 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
|
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
某市2013年10月1日—10月30日,对空气质量指数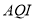 进行监测,获得数据后得到如图的条形图:
进行监测,获得数据后得到如图的条形图:
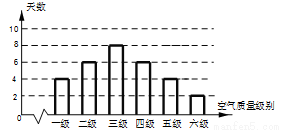
(1)估计该城市本月(按30天计)空气质量类别为中度污染的概率;
(2)在上述30个监测数据中任取2个,设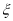 为空气质量类别颜色为紫色的天数,求
为空气质量类别颜色为紫色的天数,求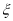 的分布列.
的分布列.
(1)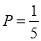 ;(2)图见解析
;(2)图见解析
【解析】
试题分析:(1)求随机变量的分布列的主要步骤:一是明确随机变量的取值,并确定随机变量服从何种概率分布;二是求每一个随机变量取值的概率,三是列成表格;(2)求出分布列后注意运用分布列的两条性质检验所求的分布列是否正确;(3)求解离散随机变量分布列和方差,首先要理解问题的关键,其次要准确无误的找出随机变量的所有可能值,计算出相对应的概率,写成随机变量的分布列,正确运用均值、方差公式进行计算.
试题解析:【解析】
(1)由条形统计图可知,空气质量类别为中度污染的天数为6,
所以该城市本月空气质量类别为中度污染的概率 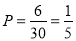 .
.
(2)随机变量 的可能取值为
的可能取值为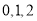 ,
,
则 ,
,
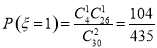 ,
,
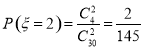
所以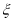 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
考点:1、求随机事件的概率;2、求离散型随机变量的分布列.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:高中数学 来源:2015届广东省惠州市高三第二次调研考试理科数学试卷(解析版) 题型:选择题
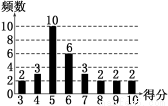
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为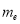 ,众数为
,众数为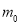 ,平均值为
,平均值为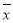 ,则( )
,则( )
A.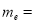
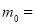
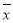 B.
B.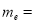
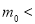
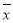
C.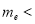
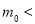
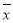 D.
D.
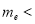
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测文科数学试卷(解析版) 题型:选择题
已知各项为正的等比数列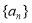 满足
满足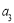 ·
·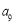 =
=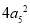 ,
,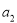 =1,则
=1,则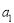 = ( )
= ( )
A.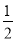 B.2 C.
B.2 C.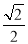 D.
D.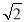
查看答案和解析>>
科目:高中数学 来源:2015届山西省忻州市高三上学期第一次四校联考理科数学试卷(解析版) 题型:选择题
已知函数 是定义在R上的偶函数,对于任意
是定义在R上的偶函数,对于任意 都
都 成立;当
成立;当 ,且
,且 时,都有
时,都有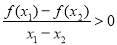 .给出下列四个命题:
.给出下列四个命题:
① ;
;
②直线 是函数
是函数 图象的一条对称轴;
图象的一条对称轴;
③函数 在
在 上为增函数;
上为增函数;
④函数 在
在 上有335个零点.
上有335个零点.
其中正确命题的个数为
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com