
分析 设|AF1|=t,则|AB|=t,|F1B|=$\sqrt{2}$t,由椭圆定义有|AF1|+|AB|+|F1B|=4a,求得|AF2|关于t的表达式,进而利用韦达定理可求得a和c的关系
解答  解:设|AF1|=t,则|AB|=t,|F1B|=$\sqrt{2}$t,由椭圆定义有:|AF1|+|AF2|=|BF1|+|BF2|=2a
解:设|AF1|=t,则|AB|=t,|F1B|=$\sqrt{2}$t,由椭圆定义有:|AF1|+|AF2|=|BF1|+|BF2|=2a
∴|AF1|+|AB|+|F1B|=4a,
化简得($\sqrt{2}$+2)t=4a,t=(4-2$\sqrt{2}$)a
∴|AF2|=2a-t=(2$\sqrt{2}$-2)a
在Rt△AF1F2中,|F1F2|2=(2c)2
∴[(4-2$\sqrt{2}$)a]2+[(2$\sqrt{2}$-2)a]2=(2c)2
∴($\frac{c}{a}$)2=9-6$\sqrt{2}$=($\sqrt{6}$-$\sqrt{2}$),
∴e=$\sqrt{6}$-$\sqrt{2}$,
故答案为:$\sqrt{6}$-$\sqrt{2}$.
点评 本题主要考查了椭圆的简单性质,考查了学生对椭圆定义的理解和运用,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
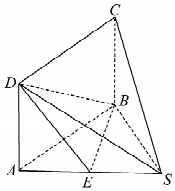 如图,在四棱锥S-ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,$SC=\sqrt{13}$.
如图,在四棱锥S-ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,$SC=\sqrt{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
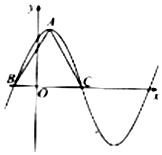 函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 单价x(元) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{7}$ | C. | $4\sqrt{7}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{4}$e3,0) | B. | [-$\frac{1}{2}$e,0) | C. | [-$\frac{1}{4}$e3,$\frac{e}{2}$) | D. | [-$\frac{1}{4}$e3,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com