（1）用综合法证明：
(
)
（2）用反证法证明：若
均为实数，且
，
，
求证：
中至少有一个大于0
科目：高中数学 来源：2015届江苏省五校高二下学期期中理科数学试卷（解析版） 题型：填空题
航空母舰“辽宁舰”将进行一次编队配置科学实验，要求2艘攻击型核潜艇一前一后，2艘驱逐舰和2艘护卫舰分列左、右，同侧不能都是同种舰艇，则舰艇分配方案的方法数为________．(用数字作答)
查看答案和解析>>
科目：高中数学 来源：2015届江苏省五校高二下学期期中文科数学试卷（解析版） 题型：填空题
求“方程
的解”有如下解题思路：设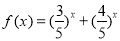
，则
在
上单调递减，且
，所以原方程有唯一解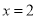
．类比上述解题思路，方程
的解为 ．
查看答案和解析>>
科目：高中数学 来源：2015届江苏省无锡江阴市高二下学期期中考试理科数学试卷（解析版） 题型：填空题
已知
的周长为
，面积为
，则的内切圆半径为
．将此结论类比到空间，已知四面体
的表面积为
，体积为
，则四面体的内切球的半径
．
查看答案和解析>>
科目：高中数学 来源：2015届江苏省扬州市高二下学期期末考试理科数学试卷（解析版） 题型：填空题
设
是
的两个非空子集，如果存在一个从
到
的函数
满足：(i)
；(ii)对任意
，当
时，恒有
.那么称这两个集合“保序同构”．现给出以下4对集合. ①
；②
；③
；④
，其中，“保序同构”的集合对的对应的序号是 (写出所有“保序同构”的集合对的对应的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（2）反证法证明,关键在于正确假设: 假设
都不大于0，则
，又
,两者矛盾，故假设错误。从而中至少有一个大于0.
------1分
------3分
------5分
时取等号
------7分
都不大于0------8分
，
，
同时成立
11分
矛盾 14分
假设不成立
原命题成立。 15分
,
,则
与
的大小关系为 ． 
，若
p是
q的充分不必要条件，则实数
的取值范围为 ．
是纯虚数，则实数
的值是__ ___ ．
”，“
”，若
是
的充分不必要条件，则
的取值范围是 ．