
分析 (Ⅰ)设C(x,y),PQ的中点K,运用圆的垂径定理和勾股定理,化简整理即可得到所求曲线E的方程;
(Ⅱ)(i)设A($\frac{{{y}_{1}}^{2}}{4}$,y1),B($\frac{{{y}_{2}}^{2}}{4}$,y2),运用向量的数量积的坐标表示,解方程可得y1y2=-20,求出直线AB的斜率,可得直线AB的方程,可令y=0,解得x=5,即可得到定点;
(ii)可令AB:x=my+5,代入抛物线方程,运用弦长公式可得|AB|,将m换为-$\frac{1}{m}$,可得|MN|,再由SAMBN=$\frac{1}{2}$|AB|•|MN|,运用换元法和基本不等式,二次函数的单调性,可得所求面积的最小值.
解答 解:(Ⅰ)设C(x,y),PQ的中点K,
则|PK|=2,CK⊥PQ,
∴|CK|2+|PK|2=|PC|2.
又|PC|=|CT|,
∴|CK|2+|PK|2=|CT|2
∴x2+4=(x-2)2+y,
整理得y2=4x.
则动圆圆心C的轨迹曲线E的方程为y2=4x;
(Ⅱ)(i)设A($\frac{{{y}_{1}}^{2}}{4}$,y1),B($\frac{{{y}_{2}}^{2}}{4}$,y2),
$\overrightarrow{OA}$•$\overrightarrow{OB}$=5得:$\frac{({y}_{1}{y}_{2})^{2}}{16}$+y1y2=5,
解得y1y2=-20(4舍去),
又有kAB=$\frac{{y}_{1}-{y}_{2}}{\frac{{{y}_{1}}^{2}}{4}-\frac{{{y}_{2}}^{2}}{4}}$=$\frac{4}{{y}_{1}+{y}_{2}}$,
AB:y-y1=$\frac{4}{{y}_{1}+{y}_{2}}$(x-$\frac{{{y}_{1}}^{2}}{4}$),
令y=0得x=-$\frac{{y}_{1}{y}_{2}}{4}$=5,
所以直线AB过定点D(5,0);
(ii)可令AB:x=my+5,
代入抛物线的方程y2=4x,可得y2-4my-20=0,
解得y=2m±$\sqrt{4{m}^{2}+20}$,
则|AB|=$\sqrt{1+{m}^{2}}$•2$\sqrt{4{m}^{2}+20}$,
将m换为-$\frac{1}{m}$,从而|MN|=$\sqrt{1+\frac{1}{{m}^{2}}}$•2$\sqrt{\frac{4}{{m}^{2}}+20}$,
∴SAMBN=$\frac{1}{2}$|AB|•|MN|=2$\sqrt{1+{m}^{2}}$•$\sqrt{1+\frac{1}{{m}^{2}}}$•$\sqrt{4{m}^{2}+20}$•$\sqrt{\frac{4}{{m}^{2}}+20}$
=2$\sqrt{2+({m}^{2}+\frac{1}{{m}^{2}})}$•$\sqrt{26+5({m}^{2}+\frac{1}{{m}^{2}})}$,
令u=m2+$\frac{1}{{m}^{2}}$(u≥2),
则SAMBN=2$\sqrt{(2+u)(26+5u)}$,
易知(2+u)(26+5u)随着u增加单调递增,
故当u=2即m2=1时,SAMBN=2$\sqrt{(2+u)(26+5u)}$的最小值为24.
点评 本题考查轨迹方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $ω=\frac{1}{2},φ=\frac{π}{4}$ | B. | $ω=2,φ=\frac{π}{4}$ | C. | $ω=\frac{1}{2},φ=\frac{π}{2}$ | D. | $ω=2,φ=\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{9}{4}$ | C. | $\frac{{2\sqrt{3}+5}}{4}$ | D. | $\frac{{2\sqrt{3}+6}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 300 | B. | 250 | C. | 200 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
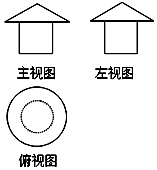 如图是一个空间几何体的三视图,其中主视图上半部分是一个底面边长为4、高为1的等腰三角形,主视图下半部分是一个边长为2的正方形,则该空间几何体的体积是( )
如图是一个空间几何体的三视图,其中主视图上半部分是一个底面边长为4、高为1的等腰三角形,主视图下半部分是一个边长为2的正方形,则该空间几何体的体积是( )| A. | $(8+2\sqrt{5})π$ | B. | $\frac{10π}{3}$ | C. | $(10+2\sqrt{5})π$ | D. | $\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
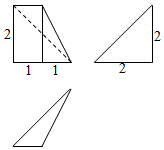
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $±\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | 0 | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com