
已知正方体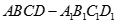 ,
, 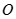 是底
是底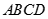 对角线的交点.
对角线的交点.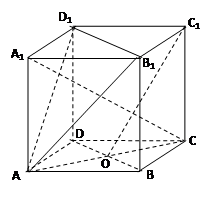
求证:(Ⅰ)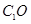 ∥面
∥面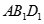 ;
;
(Ⅱ)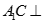 面
面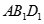
(Ⅰ)连结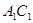 ,设
,设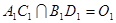 ,连结
,连结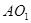 ,
,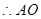

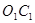 ,
, 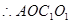 是平行四边形,
是平行四边形, 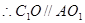 ,
,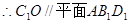 .
.
(Ⅱ)先证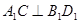 ,同理可证
,同理可证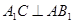 ,又
,又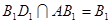 ,得到
,得到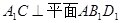 。
。
解析试题分析:(Ⅰ)连结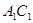 ,设
,设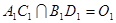 ,连结
,连结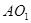 ,
,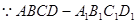 是正方体,
是正方体, 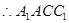 是平行四边形,
是平行四边形, 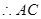

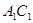 , 又
, 又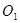 ,
,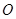 分别是
分别是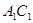 ,
,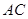 的中点,
的中点,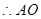

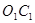 ,
, 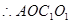 是平行四边形,
是平行四边形, 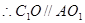 4分
4分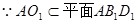 ,
,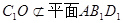
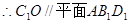 . 6分
. 6分
(Ⅱ) ,
,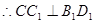 ,
,
又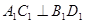 ,
, ,
, 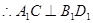 , 10分
, 10分
同理可证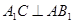 , 11分
, 11分
又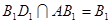 ,
,  , 13分
, 13分
考点:本题主要考查正方体的几何特征,立体几何中的平行关系、垂直关系。
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。本题主要考查正方体的几何性质,难度不大。应注意规范写出证明过程。


科目:高中数学 来源: 题型:解答题
如图(1),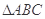 是等腰直角三角形,其中
是等腰直角三角形,其中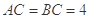 ,
,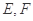 分别为
分别为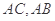 的中点,将
的中点,将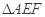 沿
沿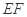 折起,点
折起,点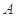 的位置变为点
的位置变为点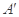 ,已知点
,已知点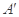 在平面
在平面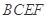 上的射影
上的射影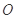 为
为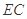 的中点,如图(2)所示.
的中点,如图(2)所示.
(1)求证: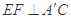 ;
;
(2)求三棱锥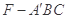 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱(侧棱垂直底面)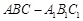 中,M、N分别是BC、AC1中点,AA1=2,AB=
中,M、N分别是BC、AC1中点,AA1=2,AB=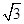 ,AC=AM=1.
,AC=AM=1.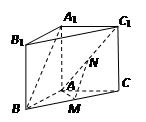
(1)证明:MN∥平面A1ABB1;
(2)求几何体C—MNA的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图甲,设正方形 的边长为
的边长为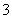 ,点
,点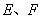 分别在
分别在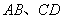 上,并且满足
上,并且满足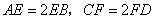 ,如图乙,将直角梯形
,如图乙,将直角梯形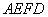 沿
沿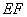 折到
折到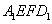 的位置,使点
的位置,使点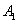 在
在
平面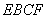 上的射影
上的射影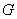 恰好在
恰好在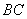 上.
上.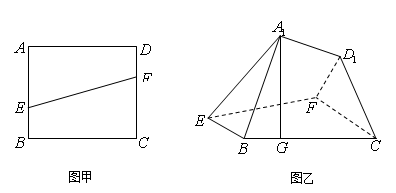
(1)证明: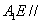 平面
平面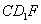 ;
;
(2)求平面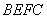 与平面
与平面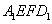 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
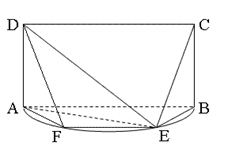
如图,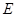 是以
是以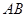 为直径的半圆上异于
为直径的半圆上异于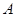 、
、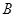 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且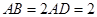 .
.
(Ⅰ)求证: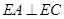 ;
;
(Ⅱ)设平面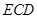 与半圆弧的另一个交点为
与半圆弧的另一个交点为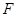 .
.
①试证: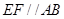 ;
;
②若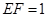 ,求三棱锥
,求三棱锥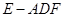 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com