
分析 根据分段函数得到${∫}_{-1}^{1}$f(x)dx=${∫}_{-1}^{0}$(x-1)dx+${∫}_{0}^{1}$(x2+1)dx,计算即可.
解答 解:${∫}_{-1}^{1}$f(x)dx=${∫}_{-1}^{0}$(x-1)dx+${∫}_{0}^{1}$(x2+1)dx=($\frac{1}{2}{x}^{2}$-x)|${\;}_{-1}^{0}$+($\frac{1}{3}{x}^{3}$+x)|${\;}_{0}^{1}$=0-($\frac{1}{2}$+1)+$\frac{1}{3}$+1=-$\frac{1}{6}$
点评 本题考查了的定积分的计算以及分段函数,属于基础题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分条件又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,5,7} | B. | {1,3,5} | C. | {3,5} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源:2017届江苏南京市高三上学期学情调研数学试卷(解析版) 题型:解答题
已知数列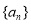 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前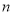 项和为
项和为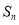 ,且
,且 ,
,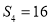 .
.
(1)求数列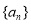 的通项公式;
的通项公式;
(2)数列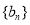 满足
满足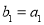 ,
,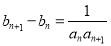 .
.
①求数列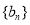 的通项公式;
的通项公式;
②是否存在正整数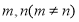 ,使得
,使得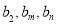 成等差数列?若存在,求出
成等差数列?若存在,求出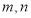 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com