
【题目】设全集为R,![]() .
.
(1)求![]() 及
及![]()
(2)若![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)A∩B={x|3<x≤5},R(A∩B)={x|x≤3或x>5},
(2)(﹣∞,![]() ]∪[6,+∞)
]∪[6,+∞)
【解析】
(1)由A={x|2<x≤5},B={x|3<x<8},能求出A∩B及R(A∩B).
(2)由A∩B={x|3<x≤5},(A∩B)∩C=,当C=时,a﹣1≥2a,当C≠时,![]() 或
或![]() ,由此能求出实数a的取值范围.
,由此能求出实数a的取值范围.
(1)因为A={x|2<x≤5},B={x|3<x<8},
所以A∩B={x|3<x≤5},
R(A∩B)={x|x≤3或x>5}.
(2)因为A∩B={x|3<x≤5},(A∩B)∩C=,
当C=时,a﹣1≥2a,解得a≤﹣1;
当C≠时,![]() 或
或![]() ,
,
解得﹣1<a![]() 或a≥6.
或a≥6.
综上,实数a的取值范围是(﹣∞,![]() ]∪[6,+∞).
]∪[6,+∞).


科目:高中数学 来源: 题型:
【题目】某公司的班车在8:00准时发车,小田与小方均在7:40至8:00之间到达发车点乘坐班车,且到达发车点的时刻是随机的,则小田比小方至少早5分钟到达发车点的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点
(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设不过原点O且斜率为![]() 的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|·|MB|=|MC|·|MD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC![]() 底面BCDE,BC=2,CD=
底面BCDE,BC=2,CD=![]() ,AB=AC
,AB=AC
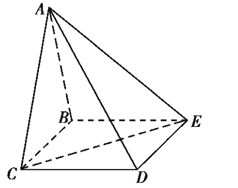
(1)证明![]() .
.
(2)设侧面ABC为等边三角形,求二面角C-AD-E的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com