Question

已知直线ax+by-1=0（a，b不全为0）与圆x²+y²=50有公共点，且公共点的横、纵坐标均为整数，那么这样的直线有（ ）
A．66条
B．72条
C．74条
D．78条

Answer 1

【答案】分析：先考虑在第一象限找出圆上横、纵坐标均为整数的点有3个，依圆的对称性知，圆上共有3×4=12个点横纵坐标均为整数，经过其中任意两点的割线有12个点任取2点确定一条直线，利用计数原理求出直线的总数，过每一点的切线共有12条，又考虑到直线ax+by-1=0不经过原点，如图所示上述直线中经过原点的有6条，所以满足题意的直线利用总数减去12，再减去6即可得到满足题意直线的条数．
解答：解：当x≥0，y≥0时，圆上横、纵坐标均为整数的点有（1，7）、（5，5）、（7，1），
根据题意画出图形，如图所示：

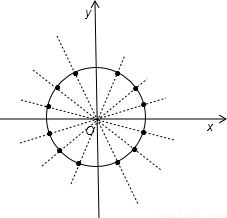
根据圆的对称性得到圆上共有3×4=12个点横纵坐标均为整数，
经过其中任意两点的割线有C₁₂²=66条，过每一点的切线共有12条，
上述直线中经过原点的有6条，如图所示，
则满足题意的直线共有66+12-6=72条．
故选B
点评：此题考查了直线与圆的位置关系，以及计数原理的运用．根据对称性找出满足题意的圆上的整数点的个数是解本题的关键．