设A, B两点的坐标分别为(－1, 0), (1, 0)，条件甲：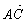
·
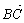＞0；条件乙：点C的坐标是方程
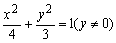的解，则甲是乙的
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
心算口算巧算一课一练系列答案科目：高中数学 来源： 题型：
某商场从生产厂家以每件20元购进一批商品，若该商品零售价定为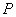
元，则销售量
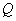（单位：件）与零售价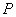（单位：元）有如下关系：
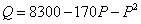，问该商品零售价定为多少元时毛利润
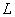最大，并求出最大毛利润．（毛利润
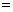销售收入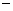
进货支出）
查看答案和解析>>
科目：高中数学 来源： 题型：
已知关于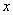
的方程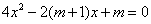
；
（1）若该方程的一根在区间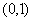
上，另一根在区间
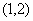上，求实数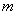
的取值范围．
（2）若该方程的两个根都在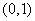
内且它们的平方和为1，求实数的取值集合．
查看答案和解析>>
科目：高中数学 来源： 题型：
设命题p：函数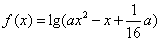
的定义域为R；命题q：不等式
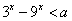对一切实数均成立。
（1）如果p是真命题，求实数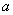
的取值范围；
（2）如果命题“p或q”为真命题，且“p且q”为假命题，求实数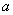的取值范围。
查看答案和解析>>
科目：高中数学 来源： 题型：
设命题p：方程x2＋3x－1＝0的两根符号不同；命题q：方程x2＋3x－1＝0的两根之和为3，判断命题“Øp”、“Øq”、“p∧q”、“p∨q”为假命题的个数为
A．0 B．1 C．2 D．3
查看答案和解析>>
科目：高中数学 来源： 题型：
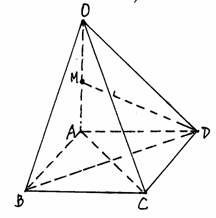
如图，在四棱锥O—ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA＝2，M为OA中点。
（1）求证：直线BD⊥平面OAC；
（2）求直线MD与平面OAC所成角的大小；
（3）求点A到平面OBD的距离。
查看答案和解析>>
科目：高中数学 来源： 题型：
已知直线l, m，平面α,β, 且l⊥α, m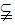
β，给出下列四个命题：
命题：
①若α∥β, 则l⊥m； ②若l⊥m, 则α∥β；
③若α⊥β，则l∥m； ④若l∥m, 则α⊥β
其中正确命题的序号是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
内投点，点落在区域的每个位置是等可能的，则坐标原点与该点连线的倾斜角小于
的概率为 。