
【题目】如图,在正三棱柱![]() 中,侧棱长和底面边长均为1,
中,侧棱长和底面边长均为1, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)试问线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,求
?若存在,求 ![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.

【答案】(1)见解析;(2) ![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(Ⅰ)连结![]() 交
交![]() 于点O,连结OD,则OD是
于点O,连结OD,则OD是![]() 的一条中位线,则
的一条中位线,则
![]() ∥OD ,即可证明
∥OD ,即可证明 ![]() ∥平面
∥平面![]()
(Ⅱ)以点D为坐标原点,DB所在直线为X轴,AD所在直线为Y轴,垂直于面ABC的直线为Z轴,建立空间直角坐标系,求出![]() 及平面ADC1的一个法向量一个法向量
及平面ADC1的一个法向量一个法向量![]() ,即可求出
,即可求出![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)假设点E在线段![]() 上,使
上,使![]() ,不妨设
,不妨设![]() (
(![]() ),通过
),通过 ![]() (1)
(1) ![]() (2)求得
(2)求得![]() 不相等,故这样的点E不存在..
不相等,故这样的点E不存在..
试题解析:(Ⅰ)连结![]() 交
交![]() 于点O,连结OD
于点O,连结OD
![]()
![]() 交
交![]() 于点O
于点O ![]() O是
O是![]() 的中点
的中点
又![]()
![]() 是
是![]() 的中点
的中点 ![]() OD是
OD是![]() 的一条中位线
的一条中位线
![]()
![]() ∥OD 又
∥OD 又![]()
![]()
![]()
![]() ∥平面
∥平面![]()

(Ⅱ)以点D为坐标原点,DB所在直线为X轴,AD所在直线为Y轴,垂直于面ABC的直线为Z轴,建立空间直角坐标系,则D(0,0,0),A(0, ![]() ,0),C(
,0),C(![]() ,0,0)
,0,0)![]()
在平面ADC1中, ![]() (0,
(0, ![]() ,0),
,0),![]()
![]()
设![]() 为平面ADC1的一个法向量,则有
为平面ADC1的一个法向量,则有 ,即
,即
不妨令![]() ,则
,则![]() ,
, ![]() ,所以
,所以![]()
又 ,则
,则![]()
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() =
= =
=![]()
![]()
![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)假设点E在线段![]() 上,使
上,使![]()
不妨设![]() (
(![]() )
)
![]()
 ,
, ![]()
![]()

![]()

![]()

![]()

![]() (0,
(0, ![]() ,0),
,0),![]()
![]()
![]()
![]() (1)
(1) ![]() (2)
(2)
由(1)可解得![]() 又(2)可解得
又(2)可解得![]() ,(1)与(2)矛盾,所以这样的点E不存在.
,(1)与(2)矛盾,所以这样的点E不存在.


科目:高中数学 来源: 题型:
【题目】下列语句是否为命题?如果是,判断它的真假.
(1)这道数学题有趣吗?(2)0不可能不是自然数;(3)![]() ;(4)
;(4)![]() ;
;
(5)91不是素数;(6)上海的空气质量越来越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗.2018年春节前夕, ![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标,检测结果如频率分布直方图所示.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标,检测结果如频率分布直方图所示.
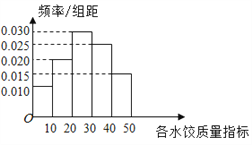
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中数据用该组区间的中点值作代表);
(同一组中数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据如下表:
的样本,得到一周参加社区服务的时间的统计数据如下表:
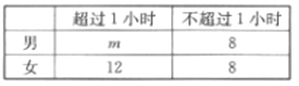
(1)求![]() ,
,![]() ;
;
(2)能否有![]() 的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
附:
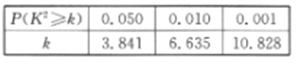
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左右焦点分别为F1,F2,点P 在椭圆上运动,
的左右焦点分别为F1,F2,点P 在椭圆上运动, ![]() 的最大值为m,
的最大值为m, ![]() 的最小值为n,且m≥2n,则该椭圆的离心率的取值范围为________
的最小值为n,且m≥2n,则该椭圆的离心率的取值范围为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年3月22日是第二十七届“世界水日”,3月22日-28日是第三十二届“中国水周”为了倡导“坚持节约用水”,某兴趣小组在本校4000名同学中,随机调查了40名同学家庭中一年的月均用水量(单位:吨),并将月均用水量分为6组:![]() ,[4,6),[6,8),[8,10),[10,12),[12,14]加以统计,得到如图所示的频率分布直方图.
,[4,6),[6,8),[8,10),[10,12),[12,14]加以统计,得到如图所示的频率分布直方图.

(1)求出图中实数a的值;
(2)根据样本数据,估计本校4000名同学家庭中,月均用水量低于8吨的约有多少户
(3)在月均用水量大于或等于10吨的样本数据中,该兴趣小组决定随机抽取2名同学的家庭进行回访,求这2名同学中恰有1人所在家庭的月均用水量属于[10,12)组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 178 | 166 | 175 | 180 |
y | 75 | 80 | 77 | 70 | 81 |
已知甲厂生产的产品共有98件.
(1)求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品,用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com