
【题目】已知函数f(x)=log2(|x+1|+|x﹣1|﹣a)
(1)当a=3时,求函数f(x)的定义域;
(2)若不等式f(x)≥2的解集为R,求实数a的最大值.
【答案】
(1)解:当a=3时,函数f(x)=log2(|x+1|+|x﹣1|﹣a)=log2(|x+1|+|x﹣1|﹣3),
∴|x+1|+|x﹣1|﹣3>0,即|x+1|+|x﹣1|>3,
∴ ![]() ①,或
①,或 ![]() ②,或
②,或 ![]() ③.
③.
解①求得x<﹣ ![]() ,解②求得x∈,解③求得x>
,解②求得x∈,解③求得x> ![]() ,
,
故函数的定义域为{x|x<﹣ ![]() ,或x>
,或x> ![]() }
}
(2)解:若不等式f(x)≥2的解集为R,则f(x)≥2恒成立,
故|x+1|+|x﹣1|﹣a≥4.
∵|x+1|+|x﹣1|≥|x+1﹣(x﹣1)|=2,
∴2﹣a≥4,故有a≤﹣2,
故实数a的最大值为﹣2
【解析】(1)由函数的解析式可得|x+1|+|x﹣1|>3,把它转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,记得所求.(2)由题意可得f(x)≥2恒成立,即|x+1|+|x﹣1|﹣a≥4 恒成立,利用绝对值三角不等式求得|x+1|+|x﹣1|的最小值为2,可得 2﹣a≥4,由此求得实数a的最大值.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mln(x+1),g(x)= ![]() (x>﹣1).
(x>﹣1).
(Ⅰ)讨论函数F(x)=f(x)﹣g(x)在(﹣1,+∞)上的单调性;
(Ⅱ)若y=f(x)与y=g(x)的图象有且仅有一条公切线,试求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,对每个正整数
,对每个正整数![]() ,有
,有![]() 或
或![]() .如这个数列可以为1,2,4,6,10….
.如这个数列可以为1,2,4,6,10….
(1)若某一项![]() 为奇数,且不为3的倍数,证明:
为奇数,且不为3的倍数,证明:![]() ;
;
(2)证明: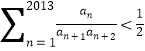 ;
;
(3)若在![]() 的前2015项中,恰有t个项为奇数,求t的最大值.
的前2015项中,恰有t个项为奇数,求t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746, 则I(a)=467,D(a)=764)阅读如右图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b= . 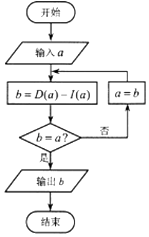
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正六边形ABCDEF的边长为2,沿对角线AE将△FAE的顶点F翻折到点P处,使得 ![]() .
. 
(1)求证:平面PAE⊥平面ABCDE;
(2)求二面角B﹣PC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由实数组成的等比数列{an}的前项和为Sn , 且满足8a4=a7 , S7=254.
(1)求数列{an}的通项公式;
(2)对n∈N* , bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N* , 存在实数x使f(x)<2成立.
(Ⅰ)求实数m的值;
(Ⅱ)若α,β>1,f(α)+f(β)=2,求证: ![]() +
+ ![]() ≥
≥ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com