
【题目】选修4-5:不等式选讲
已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N* , 存在实数x使f(x)<2成立.
(Ⅰ)求实数m的值;
(Ⅱ)若α,β>1,f(α)+f(β)=2,求证: ![]() +
+ ![]() ≥
≥ ![]() .
.
【答案】(I)解:∵|x﹣m|+|x|≥|x﹣m﹣x|=|m|, ∴要使|x﹣m|+|x|<2有解,则|m|<2,解得﹣2<m<2.
∵m∈N* , ∴m=1.
(II)证明:α,β>0,f(α)+f(β)=2α﹣1+2β﹣1=2,
∴α+β=2.
∴ ![]() +
+ ![]() =
= ![]() =
= ![]() ≥
≥ 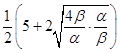 =
= ![]() ,当且仅当α=2β=
,当且仅当α=2β= ![]() 时取等号
时取等号
【解析】(I)|x﹣m|+|x|≥|x﹣m﹣x|=|m|,要使|x﹣m|+|x|<2有解,则|m|<2,m∈N* , 解得m.(II)α,β>1,f(α)+f(β)=2α﹣1+2β﹣1=2,可得α+β=2.再利用基本不等式的性质即可得出.
【考点精析】解答此题的关键在于理解基本不等式的相关知识,掌握基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(|x+1|+|x﹣1|﹣a)
(1)当a=3时,求函数f(x)的定义域;
(2)若不等式f(x)≥2的解集为R,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且过点P
,且过点P![]() 。
。
(1)求椭圆的标准方程;
(2)已知斜率为1的直线l过椭圆的右焦点F交椭圆于A.B两点,求弦AB的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于![]() 的线性回归方程;
的线性回归方程;
(2)判断y与![]() 之间是正相关还是负相关?
之间是正相关还是负相关?
(3)预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: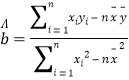 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.

(1)求证:AB∥EF;
(2)若PA=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校书法兴趣组有3名男同学A,B,C和3名女同学X,Y,Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加书法比赛![]() 每人被选到的可能性相同
每人被选到的可能性相同![]() .
.
![]() 用表中字母列举出所有可能的结果;
用表中字母列举出所有可能的结果;
![]() 设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.
设M为事件“选出的2人来自不同年级且性别相同”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是( )
A. “至少有一个黑球”与“都是红球”
B. “至少有一个黑球”与“至少有一个红球”
C. “至少有一个黑球”与“都是黑球”
D. “恰有一个黑球”与“恰有两个黑球”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|cosx|sinx+sin2x,给出下列四个命题:
①函数f(x)的图象关于直线 ![]() 对称;
对称;
②函数f(x)在区间 ![]() 上单调递增;
上单调递增;
③函数f(x)的最小正周期为π;
④函数f(x)的值域为[﹣2,2].
其中真命题的序号是 . (将你认为真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上一点
上一点![]() 与椭圆右焦点的连线垂直于x轴,直线l:y=kx+m与椭圆C相交于A,B两点(均不在坐标轴上).
与椭圆右焦点的连线垂直于x轴,直线l:y=kx+m与椭圆C相交于A,B两点(均不在坐标轴上).
(1)求椭圆C的标准方程;
(2)设O为坐标原点,若△AOB的面积为![]() ,试判断直线OA与OB的斜率之积是否为定值?若是请求出,若不是请说明理由.
,试判断直线OA与OB的斜率之积是否为定值?若是请求出,若不是请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com