Question

18．在△ABC中，若AB=3，AC=4，|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|，则$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BC}|}$的值为$\frac{12}{5}$．

Answer 1

分析 如图所示，可得平行四边形ABDC是矩形．利用直角三角形的边角关系即可得出．

解答 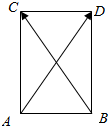解：如图所示，设$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$，
∴四边形ABDC是平行四边形
∵|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|，
∴平行四边形ABDC是矩形，
∴|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|=$\sqrt{{3}^{2}+{4}^{2}}$=5，
在Rt△ABC中，cos∠ABC=$\frac{4}{5}$，
∴$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BC}|}$=$\frac{3×5×\frac{4}{5}}{5}$=$\frac{12}{5}$，
故答案为：$\frac{12}{5}$．

点评 本题考查了向量的平行四边形法则、矩形的定义、直角三角形的边角关系，考查了推理能力与计算能力，属于中档题．