Question

【题目】已知椭圆E： =1（a＞b＞0）过点（1， ），左右焦点为F1、F2 ， 右顶点为A，上顶点为B，且|AB|= |F1F2|．
（1）求椭圆E的方程；
（2）直线l：y=﹣x+m与椭圆E交于C、D两点，与以F1、F2为直径的圆交于M、N两点，且 = ，求m的值．

Answer 1

【答案】
（1）解：椭圆E： =1（a＞b＞0）焦点在x轴上，

∵椭圆E过点 ，

∴将点（1， ），代入椭圆方程得 ，①

由已知 ，

∴ ，即a2+b2=7c2②

又∵c2=a2﹣b2③，

将①②③联立得 ，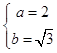

∴椭圆方程为

（2）解：根据题意，以F1、F2为直径的圆方程为x2+y2=1，

所以圆心（0，0）到直线l的距离为 ，所以|MN|= ，

设C（x1，y1），D（x1，y1），联立 ，

化简得7x2﹣8mx+4m2﹣12=0，△=48（7﹣m2）＞0，

，

由丨CD丨= ，

∴ = ，

由 得 ，

整理得 ，即 ，

经检验，当 时，△=112（7﹣m2）＞0成立，

∴

【解析】（1）由题意可知：椭圆焦点在x轴上，将点（1， ）代入椭圆方程 ，由 ，c2=a2﹣b2 ， 联立即可求得a和b的值，即可求得椭圆E的方程；（2）圆心（0，0）到直线l的距离为 ，所以|MN|= ，将直线方程方程代入椭圆方程，由韦达定理及弦长公式可知：|CD|= ，由 得 ，整理即可求得m的值．