
����Ŀ��ij������Ϊ��ʵʩ������Ч����������������������ģʽ����߹�������Ч�ʣ�ʵʩ�ˡ�������ŵ�������֡����������ͨ���ʾ�������ѧ������ְ��Ա��������Ա��250�ˣ�ͳ�ƽ�������ұ����������
ѧ�� | ��ְ��Ա | ������Ա | |
���� |
|
| 78 |
������ | 5 |
| 12 |
������������Ա�������ȡ1�ˣ�ǡ�ó鵽ѧ���ĸ���Ϊ0.32��
��1��������ѧ����������
��2�����÷ֲ�����ķ��������������Ա�г�ȡ25�ˣ�����ְ��ԱӦ��ȡ�����ˣ�
��3�����������ְ��ԱΪ77������ʾ���������д������ġ�ѧ������ְ��Ա����ѡ��2�˽��з�̸������2���а�����������Ա�ĸ��ʣ�
���𰸡�
��1���⣺������ѧ��������Ϊx��
������� ![]() =0.32��
=0.32��
���x=75��
��2���⣺��ѧ������Ϊ75+5=80��������Ա����Ϊ78+12=90��
����ְ��Ա����Ϊ250��80��90=80��
���÷ֲ�����ķ��������������Ա�г�ȡ25�ˣ�
����ְ��ԱӦ��ȡ��80�� ![]() =8�ˣ�
=8�ˣ�
��3���⣺���������ְ��ԱΪ77����������ְ��ԱΪ80��77=3�ˣ�
���ʾ���������д������ġ�ѧ������ְ��Ա����ѡ��2�˽��з�̸��
�����¼�����n= ![]() =28��
=28��
��2���а�����������Ա�����Ļ����¼�����m= ![]() =15��
=15��
����2���а�����������Ա�ĸ���p= ![]() ��
��
����������1��������ѧ��������Ϊx��������� ![]() =0.32���ɴ����������ѧ������������2����ѧ������Ϊ80��������Ա����Ϊ90������ְ��Ա����Ϊ80���ɴ�������÷ֲ�����ķ��������������Ա�г�ȡ25�ˣ���ְ��ԱӦ��ȡ����������3�����������ְ��ԱΪ77���ò��������ְ��ԱΪ3�ˣ��ɴ���������ʾ���������д������ġ�ѧ������ְ��Ա����ѡ��2�˽��з�̸����2���а�����������Ա�ĸ��ʣ�
=0.32���ɴ����������ѧ������������2����ѧ������Ϊ80��������Ա����Ϊ90������ְ��Ա����Ϊ80���ɴ�������÷ֲ�����ķ��������������Ա�г�ȡ25�ˣ���ְ��ԱӦ��ȡ����������3�����������ְ��ԱΪ77���ò��������ְ��ԱΪ3�ˣ��ɴ���������ʾ���������д������ġ�ѧ������ְ��Ա����ѡ��2�˽��з�̸����2���а�����������Ա�ĸ��ʣ�
�����㾫����ͨ��������÷ֲ�����������Ƚ������е����е�λ����ij���������־���Ա�����ȣ����ֳ��������ͻ��Σ�Ȼ�����ڸ������ͻ����в��ü����������ϵ�ó����İ취��ȡһ���������������Щ������������������������������Խ����⣮


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��x1 �� f��x1����B��x2 �� f��x2�����Ǻ���f��x��=2sin����x+�գ����أ�0���� ![]() ���գ�0��ͼ���ϵ��������㣬�ҳ���յ��ձ߾�����P��1����
���գ�0��ͼ���ϵ��������㣬�ҳ���յ��ձ߾�����P��1���� ![]() ������|f��x1����f��x2��|=4ʱ��|x1��x2|����СֵΪ
������|f��x1����f��x2��|=4ʱ��|x1��x2|����СֵΪ ![]() ��
��
��1������f��x���Ľ���ʽ��
��2����x��[0�� ![]() ]ʱ������f��x���ĵ����������䣻
]ʱ������f��x���ĵ����������䣻
��3����x��[0�� ![]() ]ʱ������ʽmf��x��+2m��f��x�����������ʵ��m��ȡֵ��Χ��
]ʱ������ʽmf��x��+2m��f��x�����������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x��lnx��ax����������ֵ�㣬��ʵ��a��ȡֵ��Χ�ǣ� ��
A.�����ޣ�0��
B.��0�� ![]() ��
��
C.��0��1��
D.��0��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��ABCD�У�����ABCD�DZ߳�Ϊ2�����Σ�����PAD�͵���ABCD����BCD=60�㣬PA=PD= ![]() ��E��BC�е㣬��Q�ڲ���PC�ϣ�
��E��BC�е㣬��Q�ڲ���PC�ϣ� 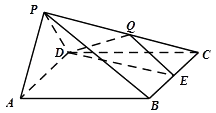
��1����֤��AD��PB��
��2����Q��PC�е㣬������E��DQ��C������ֵ��
��3���� ![]() ����PA��ƽ��DEQʱ����˵�ֵ��
����PA��ƽ��DEQʱ����˵�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λ��Ц�ǡ��ڡ�����Ц�ǡ�ѡ�����У�5λ��ί���������������ͼ��ʾ���Ǽס������˵�ƽ���÷ֱַ�Ϊ ![]() ��
�� ![]() ���Ǽס������˵÷ֵı���ֱ�Ϊs1��s2 �� �������ж���ȷ���ǣ� ��
���Ǽס������˵÷ֵı���ֱ�Ϊs1��s2 �� �������ж���ȷ���ǣ� ��
A.![]() ��
�� ![]() ��s1��s2
��s1��s2
B.![]() ��
�� ![]() ��s1��s2
��s1��s2
C.![]() ��
�� ![]() ��s1��s2
��s1��s2
D.![]() ��
�� ![]() ��s1��s2
��s1��s2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ҵ����O��ͨ����������ͱ�ƫ��30����������ֵ���ij��Pλ����ҵ���ı�ƫ��![]() �ǣ�
�ǣ�![]() ����������ҵ����O�ľ���Ϊ
����������ҵ����O�ľ���Ϊ![]() ���ﴦ����Ҫ������P��һ��ֱ·�ֱ��������ֵ�������A��B������
���ﴦ����Ҫ������P��һ��ֱ·�ֱ��������ֵ�������A��B������
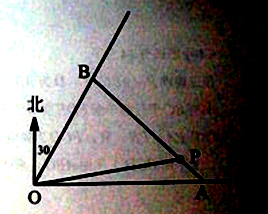
��1����AB����������ʱ��������ҵ���ĵ�A��B�����ľ���ͣ�
��2����Ҫʹ��ҵ����O��A��B�����ľ������̣���ȷ��A��B�����λ�á�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪F1��F2�ֱ�Ϊ˫���� ![]() ��a��0��b��0�������ҽ��㣬��˫������֧�ϴ���һ��Pʹ��
��a��0��b��0�������ҽ��㣬��˫������֧�ϴ���һ��Pʹ�� ![]() =8a����˫���ߵ������ʵ�ȡֵ��Χ�� ��
=8a����˫���ߵ������ʵ�ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲE�� ![]() =1��a��b��0�����㣨1��
=1��a��b��0�����㣨1�� ![]() �������ҽ���ΪF1��F2 �� �Ҷ���ΪA���϶���ΪB����|AB|=
�������ҽ���ΪF1��F2 �� �Ҷ���ΪA���϶���ΪB����|AB|= ![]() |F1F2|��
|F1F2|��
��1������ԲE�ķ��̣�
��2��ֱ��l��y=��x+m����ԲE����C��D���㣬����F1��F2Ϊֱ����Բ����M��N���㣬�� ![]() =
= ![]() ����m��ֵ��
����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪c��0��������p������y=cxΪ������������q����x��[ ![]() ��2]ʱ������f��x��=x+
��2]ʱ������f��x��=x+ ![]() ��
�� ![]() ����������p��qΪ�����⣬p��qΪ�����⣬��c��ȡֵ��Χ��
����������p��qΪ�����⣬p��qΪ�����⣬��c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com