
【题目】已知数列{an}的前n项和为Sn , 点(n, ![]() )在直线y=
)在直线y= ![]() x+
x+ ![]() 上. (Ⅰ)求数列{an}的通项公式;
上. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和为Tn , 并求使不等式Tn>
,求数列{bn}的前n项和为Tn , 并求使不等式Tn> ![]() 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
【答案】解:(Ⅰ)由题意,得 ![]() =
= ![]() ,化为Sn=
,化为Sn= ![]() . 故当n≥2时,an=Sn﹣Sn﹣1=
. 故当n≥2时,an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =n+5,
=n+5,
当n=1时,a1=S1=6=1+5,
∴an=n+5.
(Ⅱ)bn= ![]() =
= ![]() =
= ![]() ,
,
∴Tn= ![]() +…+
+…+ ![]()
= ![]() =
= ![]() .
.
由于Tn+1﹣Tn= ![]() =
= ![]() >0,
>0,
因此Tn单调递增,
故(Tn)min=1.
令1 ![]() ,解得k<20,
,解得k<20,
∴kmax=19
【解析】(Ⅰ)由题意,得 ![]() =
= ![]() ,化为Sn=
,化为Sn= ![]() . 利用递推关系即可得出.(2)利用“裂项求和”可得Tn , 再利用数列的单调性、不等式的性质即可得出.
. 利用递推关系即可得出.(2)利用“裂项求和”可得Tn , 再利用数列的单调性、不等式的性质即可得出.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,PA=PD= ![]() ,E是BC中点,点Q在侧棱PC上.
,E是BC中点,点Q在侧棱PC上. 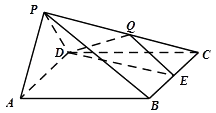
(1)求证:AD⊥PB;
(2)若Q是PC中点,求二面角E﹣DQ﹣C的余弦值;
(3)若 ![]() ,当PA∥平面DEQ时,求λ的值.
,当PA∥平面DEQ时,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ![]() ),左右焦点为F1、F2 , 右顶点为A,上顶点为B,且|AB|=
),左右焦点为F1、F2 , 右顶点为A,上顶点为B,且|AB|= ![]() |F1F2|.
|F1F2|.
(1)求椭圆E的方程;
(2)直线l:y=﹣x+m与椭圆E交于C、D两点,与以F1、F2为直径的圆交于M、N两点,且 ![]() =
= ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有红、黄、蓝三种颜色小旗各2面,将他们排成3行2列,要求每行及每列的颜色均互不相同,则不同的排列方法共有( )
A. 12种 B. 18种 C. 24种 D. 36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知c>0,设命题p:函数y=cx为减函数;命题q:当x∈[ ![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+ ![]() >
> ![]() 恒成立,如果p∨q为真命题,p∧q为假命题,求c的取值范围.
恒成立,如果p∨q为真命题,p∧q为假命题,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动(向右为顺时针,向左为逆时针).设顶点
轴滚动(向右为顺时针,向左为逆时针).设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则关于
,则关于![]() 的最小正周期
的最小正周期![]() 及
及![]() 在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com