
【题目】已知定义域为R的奇函数f(x)满足:当x>0时,f(x)=lnx,则函数g(x)=f(x)﹣sin4x的零点的个数为 .
【答案】7
【解析】解:函数f(x)=sin4x是奇函数,且它的周期为 ![]() =
= ![]() ,
,
∵g(x)=f(x)﹣sin4x=0,
∴函数g(x)=f(x)﹣sin4x的零点的个数为
相当于f(x)=sin4x的零点个数,
即f(x)与sin4x的交点个数,
∴画出二者图象,由数形结合,
可知,在(﹣∞,0)有3个交点,0处有一个交点,(0,+∞)有3个交点,
故共有7个交点.
∴函数g(x)=f(x)﹣sin4x的零点的个数为7个,
所以答案是:7.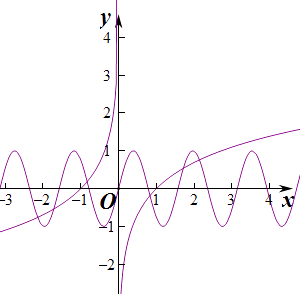
【考点精析】关于本题考查的函数奇偶性的性质,需要了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】设对于任意实数x,不等式|x+7|+|x﹣1|≥m恒成立.
(1)求m的取值范围;
(2)当m取最大值时,解关于x的不等式:|x﹣3|﹣2x≤2m﹣12.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
(Ⅰ)求证:圆心O在直线AD上;
(Ⅱ)求证:点C是线段GD的中点.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 点(n, ![]() )在直线y=
)在直线y= ![]() x+
x+ ![]() 上. (Ⅰ)求数列{an}的通项公式;
上. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和为Tn , 并求使不等式Tn>
,求数列{bn}的前n项和为Tn , 并求使不等式Tn> ![]() 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 能构成映射,下列说法正确的有 ( )
能构成映射,下列说法正确的有 ( )
(1)A中的任一元素在B中必须有像且唯一;
(2)A中的多个元素可以在B中有相同的像;
(3)B中的多个元素可以在A中有相同的原像;
(4)像的集合就是集合B.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为落实《课标》所倡导的课程理念,切实提高学生的综合素质,某校高二年级开设“趣味数学”、“趣味物理”、“趣味化学”3门任意选修课程,供年级300位文科生自由选择2门(不可多选或少选),选课情况如下表:

(Ⅰ)为了解学生选课情况,现采用分层抽样方法抽取了三科作业共50本,统计发现“趣味物理”有18本,试根据这一数据估计![]() ,
, ![]() 的值;
的值;
(Ⅱ)为方便开课,学校要求![]() ,
, ![]() ,计算
,计算![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 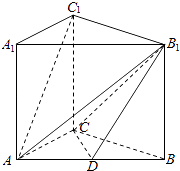
(1)求证:AC1∥平面CDB1
(2)求证:AC⊥BC1
(3)求直线AB1与平面BB1C1C所成的角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 设c1≥c2≥c3 , 则c1﹣c3=( )
,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 设c1≥c2≥c3 , 则c1﹣c3=( )
A.6
B.8
C.2
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com