
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 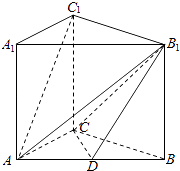
(1)求证:AC1∥平面CDB1
(2)求证:AC⊥BC1
(3)求直线AB1与平面BB1C1C所成的角的正切值.
【答案】
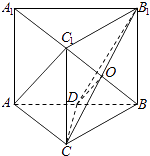
(1)解:如图:
设BC1∩B1C=O,则O为BC1的中点,连接OD,
∵D为AB的中点,∴OD∥AC1,
又∵OD平面CDB1,AC1平面CDB1,
∴AC1∥平面CDB1.
(2)解:∵AC2+BC2=AB2,∴AC⊥BC.
又∵C1C∥AA1,AA1⊥底面ABC,∴C1C⊥底面ABC,∴AC⊥CC1.
又BC∩CC1=C,∴AC⊥平面BCC1B1.
而BC1平面BCC1B1,∴AC⊥BC1.
(3)解:由(2)得AC⊥平面B1BCC1,
∴直线B1C是斜线AB1在平面B1BCC1上的射影,
∴∠AB1C是直线AB1与平面B1BCC1所成的角,
在RT△AB1C中,B1C=4 ![]() ,AC=3,
,AC=3,
∴tan∠AB1C= ![]() =
= ![]() ,
,
直线AB1与平面BB1C1C所成的角的正切值为 ![]() .
.
【解析】(1)设BC1∩B1C=O,由三角形的中位线性质可得OD∥AC1 , 从而利用线面平行的判定定理证明AC1∥平面CDB1 , (2)利用勾股定理证明AC⊥BC,证明C1C⊥底面ABC,可得AC⊥CC1 , 由线面垂直的判定定理证得AC⊥平面BCC1B1 , 从而证得AC⊥BC1 . (3)得到∠AB1C是直线AB1与平面B1BCC1所成的角,解三角形即可.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点,以及对直线与平面平行的判定的理解,了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx,sinx),
=(cosx,sinx), ![]() =(
=( ![]() sinx,sinx),x∈R设函数f(x)=
sinx,sinx),x∈R设函数f(x)= ![]() ﹣
﹣ ![]()
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长为2的线段AB中点为C,当线段AB的两个端点A和B分别在x轴和y轴上运动时,C点的轨迹为曲线C1;
(1)求曲线C1的方程;
(2)直线 ![]() ax+by=1与曲线C1相交于C、D两点(a,b是实数),且△COD是直角三角形(O是坐标原点),求点P(a,b)与点(0,1)之间距离的最小值.
ax+by=1与曲线C1相交于C、D两点(a,b是实数),且△COD是直角三角形(O是坐标原点),求点P(a,b)与点(0,1)之间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲制作容积为16米3 , 高为1米的无盖长方体容器,已知该容器的底面造价是每平方米1000元,侧面造价是每平方米500元,记该容器底面一边的长为x米,容器的总造价为y元.
(1)试用x表示y;
(2)求y的最小值及此时该容器的底面边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com