
【题目】某公司欲制作容积为16米3 , 高为1米的无盖长方体容器,已知该容器的底面造价是每平方米1000元,侧面造价是每平方米500元,记该容器底面一边的长为x米,容器的总造价为y元.
(1)试用x表示y;
(2)求y的最小值及此时该容器的底面边长.
【答案】
解:(1)由容器底面一边的长为x米,设宽为zm,
则xz1=16,即xz=16,即z=![]() ,
,
则该容器的造价y=1000xz+500(x+x+z+z)
=16000+1000(x+z)=16000+1000(x+![]() ),x>0;
),x>0;
(2)由16000+1000(x+![]() )
)
≥16000+1000×2![]()
=16000+8000=24000.
(当且仅当x=z=4时,等号成立)
故该容器的最低总价是24000元,
此时该容器的底面边长为4m.
【解析】(1)设长方体容器的长为xm,宽为zm;从而可得xz=16,从而写出该容器的造价为y=1000xz+500(x+x+z+z);
(2)利用基本不等式,可得x+![]() ≥2
≥2![]() , 即可得到所求的最值和对应的x的值.
, 即可得到所求的最值和对应的x的值.
【考点精析】关于本题考查的基本不等式在最值问题中的应用,需要了解用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 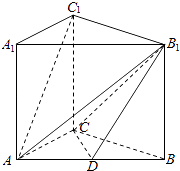
(1)求证:AC1∥平面CDB1
(2)求证:AC⊥BC1
(3)求直线AB1与平面BB1C1C所成的角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,函数
,函数![]() ,且
,且![]() 图象上一个最高点为
图象上一个最高点为![]() 与
与![]() 最近的一个最低点的坐标为
最近的一个最低点的坐标为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() 为常数,判断方程
为常数,判断方程![]() 在区间
在区间![]() 上的解的个数;
上的解的个数;
(Ⅲ)在锐角![]() 中,若
中,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x|,g(x)=lg(ax2﹣4x+1),若对任意x1∈R,都存在在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
A.(﹣∞,4]
B.(0,4]
C.(﹣4,0]
D.[0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)第1小题5分,第2小题5分,第3小题6分.
已知函数![]() ,其中
,其中![]() 为常数,且
为常数,且![]() .
.
(1) 若![]() 是奇函数,求
是奇函数,求![]() 的取值集合
的取值集合![]() ;
;
(2) 当![]() 时,设
时,设![]() 的反函数为
的反函数为![]() ,且函数
,且函数![]() 的图像与
的图像与![]() 的图像关于
的图像关于![]() 对称,求
对称,求![]() 的取值集合
的取值集合![]() ;
;
(3) 对于问题(1)(2)中的![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 设c1≥c2≥c3 , 则c1﹣c3=( )
,集合M={x|f(x)=0}={x1 , x2 , x3 , x4 , x5}N* , 设c1≥c2≥c3 , 则c1﹣c3=( )
A.6
B.8
C.2
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设偶函数f(x)的定义域为[﹣4,0)∪(0,4],若当x∈(0,4]时,f(x)=log2x,
(1)求出函数在定义域[﹣4,0)∪(0,4]的解析式;
(2)求不等式xf(x)<0得解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在2014年上半年的收入x(单位:万元)与月支出y(单位:万元)的统计资料如下表所示:
月份 | 1月份 | 2月份 | 3月份 | 4月份 | 5月份 | 6月份 |
收入x | 12.3 | 14.5 | 15.0 | 17.0 | 19.8 | 20.6 |
支出Y | 5.63 | 5.75 | 5.82 | 5.89 | 6.11 | 6.18 |
根据统计资料,则( )
A.月收入的中位数是15,x与y有正线性相关关系
B.月收入的中位数是17,x与y有负线性相关关系
C.月收入的中位数是16,x与y有正线性相关关系
D.月收入的中位数是16,x与y有负线性相关关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com