
【题目】设函数f(x)=|x|,g(x)=lg(ax2﹣4x+1),若对任意x1∈R,都存在在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
A.(﹣∞,4]
B.(0,4]
C.(﹣4,0]
D.[0,+∞)
【答案】D
【解析】x1∈R,f(x)=|x|∈[0,+∞),
∵x2∈R,使f(x1)=g(x2),
∴g(x)=lg(ax2﹣4x+1)的值域包含[0,+∞),
当a=0时,g(x)=lg(﹣4x+1),显然成立;
当a≠0时,要使g(x)=lg(ax2﹣4x+1)的值域包含[0,+∞),
则ax2﹣4x+1的最小值小于等于1,
∴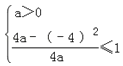 , 即a>0.
, 即a>0.
综上,a≥0.
∴实数a的取值范围是[0,+∞).
故选:D.
【考点精析】通过灵活运用函数的值域,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某公司欲制作容积为16米3 , 高为1米的无盖长方体容器,已知该容器的底面造价是每平方米1000元,侧面造价是每平方米500元,记该容器底面一边的长为x米,容器的总造价为y元.
(1)试用x表示y;
(2)求y的最小值及此时该容器的底面边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动(向右为顺时针,向左为逆时针).设顶点
轴滚动(向右为顺时针,向左为逆时针).设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则关于
,则关于![]() 的最小正周期
的最小正周期![]() 及
及![]() 在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有![]() 个红球和
个红球和![]() 个黒球的口袋内任取
个黒球的口袋内任取![]() 个球,那么互斥而不对立的两个事件是( )
个球,那么互斥而不对立的两个事件是( )
A.至少有一个黒球与都是黒球
B.至少有一个黑球与都是红球
C.至少有一个黒球与至少有![]() 个红球
个红球
D.恰有![]() 个黒球与恰有
个黒球与恰有![]() 个黒球
个黒球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com