
【题目】已知长为2的线段AB中点为C,当线段AB的两个端点A和B分别在x轴和y轴上运动时,C点的轨迹为曲线C1;
(1)求曲线C1的方程;
(2)直线 ![]() ax+by=1与曲线C1相交于C、D两点(a,b是实数),且△COD是直角三角形(O是坐标原点),求点P(a,b)与点(0,1)之间距离的最小值.
ax+by=1与曲线C1相交于C、D两点(a,b是实数),且△COD是直角三角形(O是坐标原点),求点P(a,b)与点(0,1)之间距离的最小值.
【答案】
(1)解:设C点坐标为(x,y),则A点坐标为(2x,0),B点坐标为(0,2y),由|AB|=2,得(2x﹣0)2+(0﹣2y)2=4,
化简得x2+y2=1,
所以曲线C1的方程x2+y2=1,
(2)解:由曲线C1的方程x2+y2=1可知圆心(0,0),半径为1,
所以|OC|=|OD|=1,△COD是等腰直角三角形,|CD|= ![]() ,
,
圆心(0,0)到直线 ![]() ax+by=1的距离
ax+by=1的距离 ![]() =
= ![]() ,
,
即2a2+b2=2,
所以a2=1﹣ ![]() b2,(﹣
b2,(﹣ ![]() ≤b≤
≤b≤ ![]() )
)
点P(a,b)与点(0,1)之间距离|OP|= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
当b= ![]() 时,|OP|取到最小值|OP|=
时,|OP|取到最小值|OP|= ![]() =
= ![]() ﹣1.
﹣1.
【解析】(1)设C点坐标为(x,y),根据中点坐标公式,得到A点坐标为(2x,0),B点坐标为(0,2y),由|AB|=2,即可求出曲线C1的方程,(2)先求出,△COD是等腰直角三角形,|CD|= ![]() ,再根据点到直线的距离公式得到
,再根据点到直线的距离公式得到 ![]() =
= ![]() ,再由点到点的距离公式,根据函数的性质即可求出.
,再由点到点的距离公式,根据函数的性质即可求出.


科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足:a1= ![]() ,a1 , a2 , a3﹣
,a1 , a2 , a3﹣ ![]() 成等差数列,公比q∈(0,1)
成等差数列,公比q∈(0,1)
(1)求数列{an}的通项公式;
(2)设bn=2nan , 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 能构成映射,下列说法正确的有 ( )
能构成映射,下列说法正确的有 ( )
(1)A中的任一元素在B中必须有像且唯一;
(2)A中的多个元素可以在B中有相同的像;
(3)B中的多个元素可以在A中有相同的原像;
(4)像的集合就是集合B.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() :
:![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“转点”.当
的“转点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 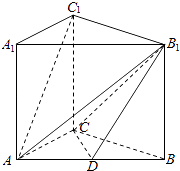
(1)求证:AC1∥平面CDB1
(2)求证:AC⊥BC1
(3)求直线AB1与平面BB1C1C所成的角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,函数
,函数![]() ,且
,且![]() 图象上一个最高点为
图象上一个最高点为![]() 与
与![]() 最近的一个最低点的坐标为
最近的一个最低点的坐标为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() 为常数,判断方程
为常数,判断方程![]() 在区间
在区间![]() 上的解的个数;
上的解的个数;
(Ⅲ)在锐角![]() 中,若
中,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)第1小题5分,第2小题5分,第3小题6分.
已知函数![]() ,其中
,其中![]() 为常数,且
为常数,且![]() .
.
(1) 若![]() 是奇函数,求
是奇函数,求![]() 的取值集合
的取值集合![]() ;
;
(2) 当![]() 时,设
时,设![]() 的反函数为
的反函数为![]() ,且函数
,且函数![]() 的图像与
的图像与![]() 的图像关于
的图像关于![]() 对称,求
对称,求![]() 的取值集合
的取值集合![]() ;
;
(3) 对于问题(1)(2)中的![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(Ⅰ)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(Ⅱ)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个球中含有编号为2的球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com