
分析 (1)利用“乘1法”与基本不等式的性质即可得出.
(2)由|2x-1|-|x-1|≤$\frac{9}{2}$,通过分类讨论利用绝对值不等式的性质即可得出.
解答 解:(1)∵a∈(0,+∞),b∈(0,+∞),a+b=2,
∴$\frac{1}{a}+\frac{4}{b}=(\frac{1}{a}+\frac{4}{b})•\frac{a+b}{2}=\frac{5}{2}+\frac{b}{2a}+\frac{2a}{b}≥\frac{5}{2}+2\sqrt{\frac{b}{2a}•\frac{2a}{b}}=\frac{5}{2}+2=\frac{9}{2}$,
∴${(\frac{1}{a}+\frac{4}{b})_{min}}=\frac{9}{2}$,此时$a=\frac{2}{3}$,$b=\frac{4}{3}$.
(2)∵$\frac{1}{a}+\frac{4}{b}≥|2x-1|-|x+1|$对?a,b∈(0,+∞)恒成立,
∴$|2x-1|-|x+1|≤\frac{9}{2}$$?\left\{{\begin{array}{l}{x≤-1}\\{-2x+1+x+1≤\frac{9}{2}}\end{array}}\right.$或$\left\{{\begin{array}{l}{-1<x≤\frac{1}{2}}\\{-2x+1-x-1≤\frac{9}{2}}\end{array}}\right.$或$\left\{{\begin{array}{l}{x>\frac{1}{2}}\\{2x-1-x-1≤\frac{9}{2}}\end{array}}\right.$
$?-\frac{5}{2}≤x≤-1$或$-1<x≤\frac{1}{2}$或$\frac{1}{2}<x≤\frac{13}{2}$,
$?-\frac{5}{2}≤x≤\frac{13}{2}$,∴$x∈[-\frac{5}{2},\frac{13}{2}]$.
点评 本题考查了基本不等式的性质、绝对值不等式的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
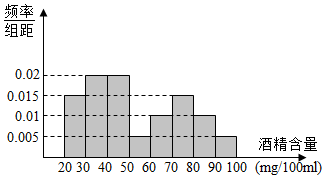 按规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含90)之间,属酒后驾车;在80mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.
按规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含90)之间,属酒后驾车;在80mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com