
分析 (1)根据绝对值不等式的解法,进行求解即可.
(2)将g(x)=$\frac{1}{f(x)+m}$的定义域为R,转化为(x)+m≠0在R上恒成立,即f(x)+m=0在R上无解,结合函数的最值进行求解即可.
解答 解:(1)由绝对值三角不等式可得,
f(x)=|2x-1|+|2x-3|≥|2x-1-2x+3|=2,
当且仅当$\left\{\begin{array}{l}{2x-1≥0}\\{2x-3≤0}\end{array}\right.$.即$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{x≤\frac{3}{2}}\end{array}\right.$,即x∈[$\frac{1}{2}$,$\frac{3}{2}$]]时等号成立,故f(x)的最小值为2.
(2)g(x)=$\frac{1}{f(x)+m}$的定义域为R等价于f(x)+m≠0在R上恒成立,
即f(x)+m=0在R上无解,所以m>-2,即实数m的取值范围为(-2,+∞).
点评 本题考查绝对值不等式的相关知识,考查考生的运算求解能力和等价转化能力.理解g(x)的定义域为R等价于f(x)+m≠0在R上恒成立是求解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
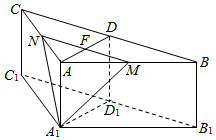 如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.
如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 000 cm3 | B. | 128 000 cm3 | C. | 150 000 cm3 | D. | 158 000 cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
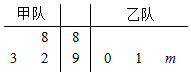 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )| A. | {2} | B. | {1,2} | C. | {0,1,2} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
| 家庭数(y) | 6 | 10 | 18 | 22 | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com