Question

10．如图（1），在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E分别是AC，AB上的点，且DE∥BC，DE=2，将△ADE沿DE折起到△A₁DE的位置，使A₁C⊥CD，如图（2）．
（1）求证：A₁C⊥平面BCDE；
（2）平面α过直线CM和点B，试作出平面α与△A₁BE的交线，并说明作法；
（3）线段BC上是否存在点P，使平面A₁DP与平面A₁BE垂直？说明理由．

Answer 1

分析 （1）证明A₁C⊥平面BCDE，因为A₁C⊥CD，只需证明A₁C⊥DE，即证明DE⊥平面A₁CD；
（2）过M作MN∥BC，交A₁E于N，连结BN，则BN即为所求的交线；
（3）设线段BC上存在点P，设P点坐标为（0，a，0），则a∈[0，3]，求出平面A₁DP法向量$\overrightarrow{{n}_{1}}$和平面A₁BE的法向量$\overrightarrow{{n}_{2}}$，假设平面A₁DP与平面A₁BE垂直，则$\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}$=0，得出a，判断是否符合条件0≤a≤3即可得出结论．

解答 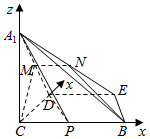（1）证明：∵BC⊥CD，DE∥BC，
∴DE⊥CD，DE⊥A₁D，又DC?平面A₁CD，A₁D?平面A₁CD，A₁D∩CD=D
∴DE⊥平面A₁CD，
∵A₁C?平面A₁CD，
∴A₁C⊥DE，又A₁C⊥CD，CD?平面BCDE，DE?平面BCDE，CD∩DE=D，
∴A₁C⊥平面BCDE．
（2）解：过M作MN∥BC，交A₁E于N，连结BN，如图：
则平面BCMN为平面α，直线BN为平面α与△A₁BE的交线．
（3）∵DE∥BC，∴$\frac{AD}{AC}=\frac{DE}{BC}$=$\frac{2}{3}$，
∴CD=2，AD=4．
∴A₁C=$\sqrt{A{D}^{2}-C{D}^{2}}$=2$\sqrt{3}$．
以C为原点建立空间直角坐标系如图：
则C（0，0，0），D（2，0，0），A₁（0，0，2$\sqrt{3}$），B（0，3，0），E（2，2，0），
设P（0，a，0）．则0≤a≤3．
∴$\overrightarrow{{A}_{1}D}$=（2，0，-2$\sqrt{3}$），$\overrightarrow{DP}$=（-2，a，0），$\overrightarrow{{A}_{1}B}$=（0，3，-2$\sqrt{3}$），$\overrightarrow{BE}$=（2，-1，0），
设平面A₁DP的法向量为$\overrightarrow{{n}_{1}}$=（x₁，y₁，z₁），平面A₁BE法向量为$\overrightarrow{{n}_{2}}$=（x₂，y₂，z₂），
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{{A}_{1}D}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{DP}=0}\end{array}\right.$，$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{{A}_{1}B}=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{BE}=0}\end{array}\right.$，
∴$\left\{\begin{array}{l}{2{x}_{1}-2\sqrt{3}{z}_{1}=0}\\{-2{x}_{1}+a{y}_{1}=0}\end{array}\right.$，$\left\{\begin{array}{l}{3{y}_{2}-2\sqrt{3}{z}_{2}=0}\\{2{x}_{2}-{y}_{2}=0}\end{array}\right.$，
∴令z₁=1得$\overrightarrow{{n}_{1}}$=（$\sqrt{3}$，$\frac{2\sqrt{3}}{a}$，1），令x₂=1得$\overrightarrow{{n}_{2}}$=（1，2，$\sqrt{3}$）．
假设平面A₁DP与平面A₁BE垂直，则$\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}$=0，
∴$\sqrt{3}$+$\frac{4\sqrt{3}}{a}$+$\sqrt{3}$=0，解得a=-2．不符合题意．
∴线段BC上不存在点P，使平面A₁DP与平面A₁BE垂直．

点评 本题考查了线面垂直的判定，面面垂直的判定，属于中档题．