
分析 ①利用分段函数的表达式,利用代入法进行求解即可.
②作出函数f(x)的图象,利用数形结合进行求解即可.
解答 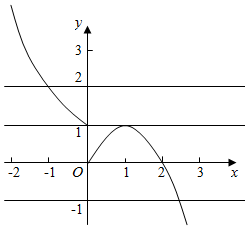 解:①由分段函数的表达式得f(-1)=2-(-1)=2,f(2)=a+1,
解:①由分段函数的表达式得f(-1)=2-(-1)=2,f(2)=a+1,
则由f(f(-1))=0,得f(2)=a+1=0,得实数a=-1;
②在①的条件下,a=-1,则f(x)=$\left\{\begin{array}{l}{-(x-1)^{2}+1,}&{x≥0}\\{{2}^{-x},}&{x<0}\end{array}\right.$,
作出函数f(x)的图象如图
由图象知当x<0时,函数f(x)为单调递减函数,且f(x)>1,
当x≥0时,f(x)≤1,
∴要使直线y=m与y=f(x)的图象有且只有一个交点,则m≥1或m<0,
即实数m的取值范围是(-∞,0)∪[1,+∞),
故答案为:-1;(-∞,0)∪[1,+∞)
点评 本题主要考查分段函数的表达式的应用,利用代入法以及数形结合是解决本题的关键.难度不大.


科目:高中数学 来源: 题型:解答题
 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?φ∈R,函数f(x)=sin(2x+φ)是奇函数 | B. | ?φ∈R,函数f(x)=sin(2x+φ)不是偶函数 | ||
| C. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 | D. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
| 家庭数(y) | 6 | 10 | 18 | 22 | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com