
| A. | (3,1)(-2,1) | B. | (0,1)(1,1) | C. | (1,0)(-1,0) | D. | (1,2)(-1,2) |
分析 可作出图形,并设平行于x轴的直线为y=m,(0<m<3),从而可得出$AB=2\sqrt{3-m}$,这样即可求得${S}_{△ABO}=\sqrt{3-m}•m$,可设$f(m)=\sqrt{3-m}•m(0<m<3)$,根据导数即可得出m=2时f(m)取到最大值,即△ABO的面积达到最大值,从而便可得出A,B两点的坐标.
解答 解:如图,设平行于x轴的直线方程为y=m(0<m<3),带入y=3-x2得,$x=±\sqrt{3-m}$;
∴$AB=2\sqrt{3-m}$;
∴${S}_{△ABO}=\sqrt{3-m}•m$;
设$f(m)=\sqrt{3-m}•m$,$f′(m)=\frac{3(2-m)}{2\sqrt{3-m}}$,0<m<3;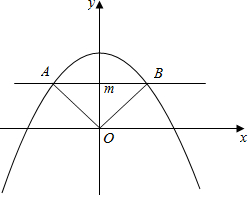
∴0<m<2时,f′(m)>0,2<m<3时,f′(m)<0;
∴m=2时,f(m)取得最大值2;
即此时△ABO的面积达到最大值;
∴此时A,B点的坐标分别为(-1,2),(1,2).
故选D.
点评 考查直线和曲线交点的坐标与直线方程和曲线方程形成方程组解的关系,二次函数图象的平移变换,三角形的面积公式,以及根据函数导数符号判断函数取得最值的方法,注意正确求导.


科目:高中数学 来源: 题型:解答题
 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
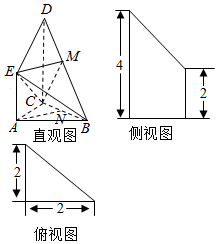 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
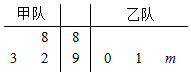 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )| A. | {2} | B. | {1,2} | C. | {0,1,2} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?φ∈R,函数f(x)=sin(2x+φ)是奇函数 | B. | ?φ∈R,函数f(x)=sin(2x+φ)不是偶函数 | ||
| C. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 | D. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com